Question

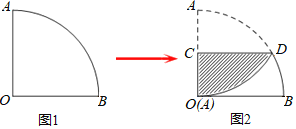
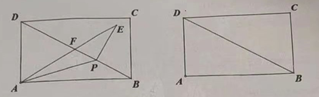
【题目】如图，把某矩形纸片ABCD沿EF，GH折叠（点E，H在AD边上，点F，G在BC边上），使点B和点C落在AD边上同一点P处，A点的对称点为A′点，D点的对称点为D′点，若∠FPG＝90°，△A′EP的面积为5，△D′PH的面积为20，则矩形ABCD的面积等于_____．

Answer 1

【答案】50+30

【解析】

设AB=CD=x，由翻折可知：PA′=AB=x，PD′=CD=x，因为△A′EP的面积为5，△D′PH的面积为20，推出D′H =4 A′E，设A′E =a，则D′H=4a，由△A′EP∽△D′PH，推出，可得x=2a，再利用三角形的面积公式求出a即可解决问题．

∵四边形ABC是矩形，

∴AB=CD，AD=BC，设AB=CD=x，

由翻折可知：PA′=AB=x，PD′=CD=x，

易证△A′EP∽△D′PH，

∵△A′EP的面积为5，△D′PH的面积为20，

∴

∴D′H =4 A′E，设A′E=a，则D′H=4a，

∵△A′EP∽△D′PH，

∴，

∴，

∴x2=4a2，

∴x=2a或-2a（舍弃），

∴PA′=PD′=2a，

∵×a×2a=5，

∴a=，

∴x=2，

∴AB=CD=2，PE==5，PH=，

∴AD=+5+10+4=15+5，

∴矩形ABCD的面积=2（15+5）=50+30．

故答案为: 50+30．