题目内容
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
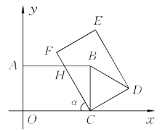
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
【答案】(1)H(2,4);(2)△CBD为等边三角形;理由见解析. (3) y=-![]() x+
x+![]() .
.
【解析】
(1)根据矩形的性质得OA=BC=4,AB=OC=6,由已知条件可知△HBC是等腰直角三角形,故可求AH=2,即可求出H的坐标;
(2)根据α=60°,得∠BCD=∠α=60°,又BC=DC即可证明△BCD是等边三角形;
(3)设AH=CH=x,则在RtΔBCH中由勾股定理代入数进行计算即可得到AH的长,进而得到H点坐标,设HC:y=kx+b(k≠0),再把C与H的坐标代入求解即可.
解:(1)H(2,4)
∵A(0,4),C(6,0),四边形OCBA为矩形,
![]() OA=BC=4,AB=OC=6
OA=BC=4,AB=OC=6
∵α=45°,∠ABC=90°,
![]() △HBC是等腰直角三角形,BH=BC=4,
△HBC是等腰直角三角形,BH=BC=4,
![]() AH=AB-BH=6-4=2,
AH=AB-BH=6-4=2,
![]() H(2,4).
H(2,4).
(2)△CBD为等边三角形
∵α=60°,
![]() ∠BCD=∠α=60°
∠BCD=∠α=60°
又∵BC=DC,
![]() △CBD为等边三角形
△CBD为等边三角形
(3)设AH=CH=x,则在RtΔBCH中由勾股定理可得x2=(6-x)2+42,解得x=![]() .故H(
.故H(![]() ,4).
,4).
设HC:y=kx+b(k≠0),则有 解得
解得
∴直线HC的解析式为y=-![]() x+
x+![]() .
.

练习册系列答案
相关题目