Question

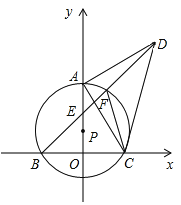
【题目】如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，连接AC、FC．

（1）求证：∠ACF=∠ADB；

（2）若点A到BD的距离为m，BF+CF=n，求线段CD的长；

（3）当⊙P的大小发生变化而其他条件不变时，的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．

Answer 1

【答案】见解析

【解析】

（1）连接AB，根据线段垂直平分线性质求出AB=AC=AD，推出∠ADB=∠ABD，根据∠ABD=∠ACM求出即可；

（2）过点A作AH⊥BD于点H，求得∠FCD=∠FDC，根据勾股定理和等腰直角三角形的性质求出CD的平方，即可求出答案；

（3）过点D作DH⊥AO于N，过点D作DQ⊥BC于Q根据AAS证△DAM ≌△ACO和△DAF ≌△CAF，推出DH=AO，AH=OC，推出DQ=BQ，得出∠DBQ=45°，推出∠HDE=45°，得出等腰直角三角形DHE即可.

解：（1）证明：∵ PO⊥BC

∴ BO=CO

∴ AO垂直平分BC

∴ AB=AC

又∵ △ACD是以AC为直角边作等腰直角三角形

∴ AC= AD

∴ AB= AD

∴ ∠ABD=∠ADB

∵ ∠ABD=∠ACF

∴ ∠ACF =∠ADB

解：（2）过点A作AH⊥BD于点H

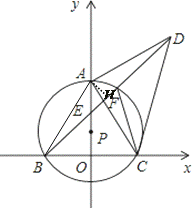
∴ AH=1

∵ △ACD是以AC为直角边作等腰直角三角形

∴ ∠ACD=∠ADC

∵ ∠ACF =∠ADB

∴∠ACD－∠ACF =∠ADC－∠ADB

即：∠FCD=∠FDC

∴ CF =DF

∵ BF+CF=14

∴ BD= BF+ DF = BF+CF =14

又∵ AB= AD

∴ BH= DH=BD=7

∴在Rt△ADH中：AD=

∴ AC= AD

∴ CD=

解：（3）的值不发生变化，过点过点D作DM⊥y轴于点M

∴ ∠DMA=∠AOC=90°

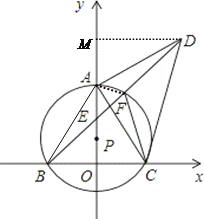
∴ ∠OAC+∠ACO=90°

∵ △ACD是以AC为直角边作等腰直角三角形

∴ ，∴ ∠DAC=90°，AC= AD

∴ ∠DAM +∠OAC = 90°

∴∠DAM=∠ACO

∴ △DAM ≌△ACO

∴ DM=AO

在△DAF与△CAF中，

AD=AC，AF=AF，DF=CF，

∴ △DAF ≌△CAF

∴ ∠DAF=∠CAF = 45°

∴ ∠CBF=∠CAF = 45°

∴ ∠BEO = 45°

∴ ∠DEM=∠BEO = 45°

∴ △DEM是等腰直角三角形

∴

∴

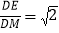
“点睛”本题考查了等腰直角三角形，全等三角形的性质和判，及勾股定理，线段垂直平分线性质，解（1）小题的关键是求出AB=AC=AD，解（2）小题的关键是求出BH的长，解（3）小题的关键是证出△DEM是等腰直角三角形.