题目内容
【题目】如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将ABCO绕点A逆时针旋转60°,得到对应的ADEF,解答下列问题: 
(1)画出旋转后的ADEF(不写作法,不证明,保留作图痕迹);
(2)求ABCO旋转过程中扫过的区域的面积.
【答案】
(1)解:如图所示,ADEF即为所求;
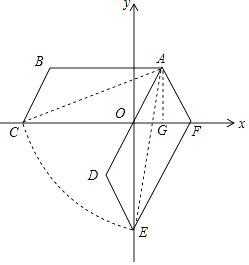
(2)解:过点A作AG⊥x轴于点G,
∵AB∥OC,∠BAO=60°,
∴∠AOG=60°,
∴OG= ![]() AO=1,AG=AOsin60°=
AO=1,AG=AOsin60°= ![]() ,
,
∴S平行四边形ABCO=ABAG=4 ![]() .
.
在Rt△ACG中,AC2=AG2+CG2=( ![]() )2+(4+1)2=28,
)2+(4+1)2=28,
∴S扇形ACE= ![]() π×AC2=
π×AC2= ![]() ,
,
∴ABCO旋转过程中扫过的区域的面积=S平行四边形ABCO+S扇形ACE=4 ![]() +
+ ![]()
【解析】(1)根据图形旋转的性质画出旋转后的ADEF即可;(2)过点A作AG⊥x轴于点G,根据锐角三角函数的定义得出OG与AG的长,再由∴ABCO旋转过程中扫过的区域的面积=S平行四边形ABCO+S扇形ACE即可得出结论.
【考点精析】本题主要考查了平行四边形的性质和扇形面积计算公式的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

练习册系列答案
相关题目






