题目内容
【题目】如图，已知抛物线y=﹣ 
x2+bx+c与x轴相交于点A，B（4，0），与y轴相交于点C，直线y=﹣x+3经过点C，与x轴相交于点D．
（1）求抛物线的解析式；
（2）点P为第一象限抛物线上一点，过点P作x轴的垂线，垂足为点E，PE与线段CD相交于点G，过点G作y轴的垂线，垂足为点F，连接EF，过点G作EF的垂线，与y轴相交于点M，连接ME，MD，设△MDE的面积为S，点P的横坐标为t，求S与t的函数关系式；
（3）在（2）的条件下，过点B作直线GM的垂线，垂足为点K，若BK=OD，求：t值及点P到抛物线对称轴的距离．
【答案】
（1）
解：对于直线y=﹣x+3，令x=0得y=3，
∴C（0，3），把B（4，0），C（0，3）的坐标代入y=﹣ 
x2+bx+c得 
，解得 
，
∴抛物线的解析式为y=﹣ x2+ 
x+3
（2）
解：如图1中，当0＜t＜ 
时，P（t，﹣ t+ t+3），
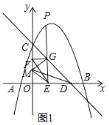
∵FG⊥OC，GE⊥OD，CO⊥OD，
∴四边形FOGE是矩形，
∴OE=FG=t，GE=GD=3﹣t，
∵MG⊥FE，FG⊥GE，
∴∠GEF+∠GFE=90°，∠GFE+∠FGM=90°，
∴∠GEF=∠FGM，
在Rt△FGE中，tan∠FEG= 
= 
，
∴在Rt△FGM中，tan∠FGM= 
= ，
∴FM= 
，
∴OM=FO﹣FM=（3﹣t）﹣ = 
，
∴S= 
DEOM= ×（3﹣t）× = ，
当 ＜t＜3时，S= DEOM= DE（FM﹣OF）= 
．
综上所述，S=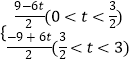 
（3）
解：如图2中，过点C作x轴的平行线，过点B作y轴的平行线，两直线交于点Q，延长MK与CQ交于点N，延长KM与x轴交于点Z，
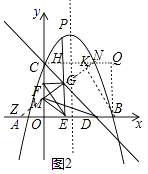
∵CQ∥BO，BQ∥CO，
∴四边形COBQ是平行四边形，
∵∠COB=90°，
∴四边形COBQ是矩形，
∴∠CQB=90°=∠BKN，CO=BQ=3，
对于直线y=﹣x+3，令y=0得x=3，
∴D（0，3），
∴OD=OC=BQ=3，
∵BK=OD，
∴BK=BQ，∵BN=BN，
∴Rt△KBN≌Rt△QBN，
∴∠KNB=∠QNB，
∵NQ∥OB，
∴∠QNB=∠NBO=∠KNB，
∴ZN=ZB，设EG交CQ于H，
∵OC=OB，
∴∠OCD=∠ODC，
∵CQ∥OB，
∴∠QHG=∠HEO=90°，∠HCD=∠CDO，
∴∠OCD=∠HCD，
∵GF⊥OC，GH⊥CH，
∴GH=GF，
∵GM⊥EF，GH⊥HN，
∴∠GEM+∠MGE=90°，∠HGN+∠HNG=90°，
∵∠HGN=∠MGE，
∴∠GEM=∠HNG，
∵∠GFO=∠FOE=∠OEG=90°，
∴∠GEF=90°=∠GHN，
∴△HNG≌△FGE，
∴CH=OE=t=GH，HN=GE=3﹣t，
∴CN=3﹣t+3=3，
∴NQ=BD=1=NK，设ZK=m，则ZB=ZN=m+1，
在Rt△KZB中，（m+1）2=m2+32，
∴m=4，
∴ZB=5，
∴tan∠GZB= ，tan∠GEF= ，
∴ = ，
∴t= 
，
∵抛物线的对称轴x= ，
∴点P到抛物线的对称轴的距离为 ﹣ = 
【解析】（1）求出点C坐标，利用待定系数法转化为方程组解决问题．（2）分两种情形①当0＜t＜ 时，P（t，﹣ t+ t+3），②当 ＜t＜3时，分别求出OM的长即可解决问题．（3）如图2中，过点C作x轴的平行线，过点B作y轴的平行线，两直线交于点Q，延长MK与CQ交于点N，延长KM与x轴交于点Z，Rt△KBN≌Rt△QBN，推出∠KNB=∠QNB，由NQ∥OB，推出∠QNB=∠NBO=∠KNB，推出ZN=ZB，设EG交CQ于H，由△HNG≌△FGE，推出CH=OE=t=GH，HN=GE=3﹣t，推出CN=3﹣t+3=3，推出NQ=BD=1=NK，设ZK=m，则ZB=ZN=m+1，在Rt△KZB中，（m+1）2=m2+32 ， 推出m=4，推出ZB=5，于tan∠GZB= ，tan∠GEF= ，可得 = ，求出t即可解决问题．
