题目内容
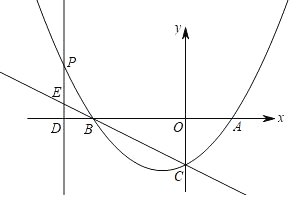
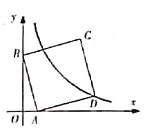
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,以
两点,以![]() 为边在第一象限作正方形
为边在第一象限作正方形![]() 沿
沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度后,点
个单位长度后,点![]() 恰好落在双曲线上,则
恰好落在双曲线上,则![]() 的值是__________.
的值是__________.
【答案】![]()
【解析】
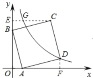
作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F,易证△OAB≌△FDA≌△BEC,求得A、B的坐标,根据全等三角形的性质可以求得C、D的坐标,从而利用待定系数法求得反比例函数的解析式,进而求得G的坐标,则a的值即可求解.
作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.
在y=3x+3中,令x=0,解得:y=3,即B的坐标是(0,3).
令y=0,解得:x=1,即A的坐标是(1,0).
则OB=3,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
又∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,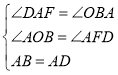
∴△OAB≌△FDA(AAS),
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=3,DF=OA=BE=1,
故D的坐标是(4,1),C的坐标是(3,4).代入y=![]() 得:k=4,则函数的解析式是:y=
得:k=4,则函数的解析式是:y=![]() .
.
∴OE=4,
则C的纵坐标是4,把y=4代入y=![]() 得:x=1.即G的坐标是(1,4),
得:x=1.即G的坐标是(1,4),
∴CG=2.
故答案为:2.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目