题目内容
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
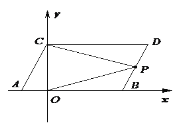
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
【答案】(1)(-1,-4);y=x-3;(0,-3);(-1,-4);)(2)①m=-![]() ; ②m=-2
; ②m=-2
【解析】试题分析:(1)、由抛物线的顶点式可求得其顶点坐标,由伴随直线的定义可求得伴随直线的解析式,联立伴随直线和抛物线解析式可求得其交点坐标;(2)、①、可先用m表示出A、B、C、D的坐标,利用勾股定理可表示出AC2、AB2和BC2,在Rt△ABC中由勾股定理可得到关于m的方程,可求得m的值;②、由B、C的坐标可求得直线BC的解析式,过P作x轴的垂线交BC于点Q,则可用x表示出PQ的长,进一步表示出△PBC的面积,利用二次函数的性质可得到m的方程,可求得m的值.
试题解析:(1)、(-1,-4);y=x-3;(0,-3);(-1,-4)
(2)、①因为抛物线解析式为![]() ,所以其伴随直线为
,所以其伴随直线为![]() ,即
,即![]() 。
。
联立抛物线与伴随直线的解析式可得:![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
在![]() 中,令
中,令![]() 可计算出
可计算出![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() (抛物线开口向下,舍去),
(抛物线开口向下,舍去),![]() ,
,
所以当![]() 时,
时,![]() ;
;
②设直线![]() 的解析式为
的解析式为![]() ,如图过
,如图过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,如图所示:
,如图所示:
因为点![]() 的横坐标为
的横坐标为![]() ,所以
,所以![]() ,
,![]() ,因为
,因为![]() 是直线
是直线![]() 上方抛物线上的一个动点,
上方抛物线上的一个动点,
所以![]()
![]()
![]() ,
,
所以,![]() 。
。
当![]() 时,
时,![]() 的值有最大值
的值有最大值![]() ,所以
,所以![]() 取得最大值
取得最大值![]() 时,即
时,即![]() ,计算得出
,计算得出![]() .
.

练习册系列答案
相关题目