题目内容
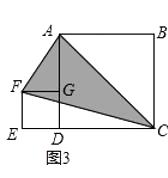
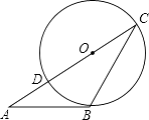
【题目】如图，小明准备测量一段水渠的深度，他把一根竹竿AB竖直插到水底，此时竹竿AB离岸边点C处的距离
米。竹竿高出水面的部分AD长0.5米，如果把竹竿的顶端A拉向岸边点C处，竿顶和岸边的水面刚好相齐，则水渠的深度BD为（ ）
A. 2米B. 2.5米C. 2.25米D. 3米
【答案】A
【解析】
经分析知：可以放到一个直角三角形中计算．此直角三角形的一条直角边CD是1.5米，另一条直角边是水渠深BD设为x米，斜边BC是竹竿的长（x+0.5）米．根据勾股定理得x2+1.52=(x+0.5)2，即可解答．
解：若假设水渠深BD设为x米，则竹竿BC的长(x+0.5)米，由题意得，
x2+1.52=(x+0.5)2，
解之得：x=2.
故选A．
练习册系列答案
寒假学与练系列答案
相关题目
【题目】在《科学》课上，老师讲到温度计的使用方法及液体的沸点时，好奇的王红同学准备测量食用油的沸点，已知食用油的沸点温度高于水的沸点温度（
），王红家只有刻度不超过的温度计，她的方法是在锅中倒入一些食用油，用煤气灶均匀加热，并每隔
测量一次锅中油温，测量得到的数据如下表：
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现，烧了
时，油沸腾了，则下列说法不正确的是（ ）
A. 没有加热时，油的温度是
B. 加热
，油的温度是
C. 估计这种食用油的沸点温度约是
D. 每加热，油的温度升高
