题目内容
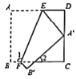
【题目】已知：如图，△ABC 中，AD⊥BC 于点 D，BE 是∠ABC 的平分线，若∠DAC=30°，∠BAC=80°，求：∠AOB 的度数．
【答案】AOB 110°．
【解析】
由AD⊥BC利用三角形内角和定理结合∠DAC=30°即可得出∠C=60°、∠ABC=40°，再根据角平分线定义可得出∠ABE=20°，在△AOB中根据三角形内角和定理即可得出∠AOB的度数．
∵ AD BC，
∴ ADC 90，
∵∠DAC 30，
∴ C 60，
∵ BAC 80 ，∠DAC 30，
∴ BAD 50，
又∵在△ABC 中， C 60 °， BAC 80 °，
∴ ABC 180 C BAC =40°，
∵BE 是∠ABC 的平分线，
∴ ABO CBO 20 °，
又∵在△ABO 中， BAO 50 °， ABO 20°，
∴ AOB 180 ABO BAO =110°．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
