题目内容
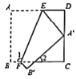
【题目】如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.
(1)求证:CD=BE;
(2)若AB=12,试求BF的长.

【答案】(1)证明见解析;(2)4.
【解析】
(1)先作DM∥AB,交CF于M,可得△CDM为等边三角形,再判定△DMF≌△EBF,最后根据全等三角形的性质以及等边三角形的性质,得出结论;
(2)根据CD⊥AC,∠A=60°=∠ABC,可得∠E=∠BFE=∠DFM=∠FDM=30°,由此得出CM=MF=BF=![]() BC,最后根据AB=12即可求得BF的长.
BC,最后根据AB=12即可求得BF的长.
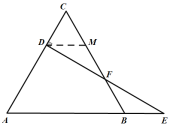
(1)证明:如图,作DM∥AB,交CB于M,则∠DMF=∠EBF.
∵△ABC是等边三角形,
∴∠C=60°=∠CDM=∠CMD,
∴△CDM是等边三角形,
∴CD=DM.
在△DMF和△EBF中,
∠DMF=∠EBF,
∠DFM=∠EFB,
DF=EF,
∴△DMF≌△EBF(AAS).
∴DM=BE,
∴CD=BE.
(2)解:∵ED⊥AC,∠A=60°=∠ABC,
∴∠E=∠BFE=∠DFM=∠FDM=30°,
∴BE=BF,DM=FM.
由(1)知△DMF≌△EBF,
∴MF=BF,
∴CM=MF=BF.
又∵AB=BC=12,
∴CM=MF=BF=4.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目