题目内容
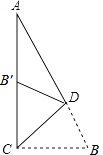
【题目】已知△ABC是等腰直角三角形,AB=![]() ,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
(1)求△ABC与△DEF的顶点坐标;
(2)判断△PEC的形状;
(3)求△PEC的面积.

【答案】(1) A(0,1),B(-1,0),C(1,0),D(1,1),E(0,0),F(2,0);(2)△PEC是等腰直角三角形;(3)S△PEC=![]() .
.
【解析】整体分析:
(1)根据勾股定理和平移的性质求出△ABC与△DEF的顶点到点E的距离或到点A的距离;(2)根据平移的性质得DE∥AB,即可判断△PEC的形状;(3)△PEC的面积等于两条直角边乘积的一半.
解:(1)连接AE,CD.
∵△ABC是等腰直角三角形,E是BC的中点,
∴AE⊥BC,∴AE2+CE2=2CE2=AC2,∴CE=![]() AC.
AC.
∵△DEF是由△ABC平移得到的,
∴CE=AE=BE=CF=CD=![]() AC=
AC=![]() ×
×![]() =1,EF=2CE=2.
=1,EF=2CE=2.
∴A(0,1),B(-1,0),C(1,0),D(1,1),E(0,0),F(2,0).
(2)根据平移的性质,可知DE∥AB,
∴∠PEC=∠B=45°,∠EPC=∠A=90°,
∴△PEC是等腰直角三角形.
(3)S△PEC=![]() PC·PE=
PC·PE=![]() PC2=
PC2=![]() ×
×![]() CE2=
CE2=![]() .
.
所以S△PEC=![]() .
.

练习册系列答案
相关题目