题目内容
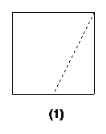
【题目】(1)如图(1),在正方形一边上取中点,并沿虚线剪开,用两块图形拼一拼,能否拼出平行四边形、梯形或三角形?画图解释你的判断.
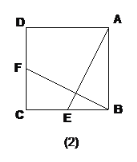
(2)如图(2)E为正方形ABCD边BC的中点,F为DC的中点,BF与AE有何关系?请解释你的结论。
【答案】(1)能;(2)AE=BF,AE⊥BF.
【解析】
(1)将三角形平移到左边与正方形左边的边重合可拼出平行四边形;将三角形旋转180度,再将三角形直角边与正方形直角边重合能拼成梯形;将三角形翻折,平移到正方形下方的边能拼成三角形;
(2)根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AMB的度数,根据直角三角形锐角的关系,可得∠ABM与∠BAM的关系,根据同角的余角相等,可得∠BAM与∠CBF的关系,根据ASA,可得△ABE≌△BCF,根据全等三角形的性质,可得答案;
(1)如图,能拼成.
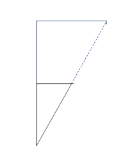
可以拼出平行四边形,将三角形平移到左边与正方形左边的边重合因为是中点,所以拼接后的上下两边相等且平行为平行四边形.
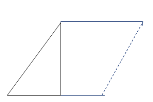
可以拼成梯形,将三角形旋转180度,再将三角形直角边与正方形直角边重合则上下两边平行,则为梯形.
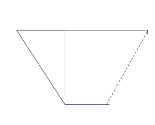
可以拼成三角形,将三角形翻折,平移到正方形下方的边重合因为是中点,所以两边相等,可以重合,为直角三角形.
(2)证明:如图,
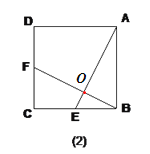
∵四边形ABCD是正方形,
∴∠ABC=∠C,AB=BC.
∵AE⊥BF,
∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,
∴∠BAM=∠CBF.
∵∠BAE+AEB=90°,
∴∠CBF+AEB=90°,
∴∠BOF=90°,
∴AE⊥BF.
在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(ASA),
∴AE=BF,
∴AE=BF,AE⊥BF.

【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?