题目内容
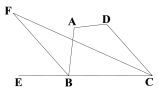
【题目】如图,已知直线y=2x+b交x轴于点A(﹣2,0),交y轴于点B,直线y=2交AB于点C,交y轴于点D,P是直线y=2上一动点,设P(m,2).
(1)求直线AB的解析式和点B,点C的坐标;
(2)直接写出m为何值时,△ABP是等腰三角形;
(3)求△ABP的面积(用含m的代数式表示).

【答案】(1)B(0,4),C(﹣1,2);(2)m=﹣4或﹣6或2或4;(3)△ABP的面积S=![]()
【解析】
(1)将点A的坐标代入y=2x+b可求出b=4,即可得AB解析式及B点坐标,把y=2代入AB解析式即可得C点坐标;(2)分AB=AP、AB=BP、AP=BP三种情况,分别求解即可;(3)根据△ABP的面积=![]() PC×OB,即可求解.
PC×OB,即可求解.
(1)将点A(-2,0)代入y=2x+b得:0=2×(﹣2)+b,
解得:b=4,
∴直线AB的表达式为:y=2x+4,
∵AB与y轴交于B,
∴B(0,4),
当y=2时,2x+4=2,
解得x=﹣1,
∴C(﹣1,2);
(2)点A(﹣2,0)、点B(0,4),点P(m,2),
∴AB2=20,AP2=(m+2)2+4,PB2=m2+4,
①当AB=AP时,即20=(m+2)2+4,
解得:m=2或﹣6,
②当AB=BP时,即20=m2+4,
解得m=4或﹣4,
③当AP=BP时,即(m+2)2+4=m2+4,
解得:m=﹣1(与点C重合,舍去),
综上,m=﹣4或﹣6或2或4;
(3)如图所示,点C(﹣1,2),则PC=|m+1|,
△ABP的面积S=![]() PC×BD+
PC×BD+![]() PC×OD=
PC×OD=![]() PC×OB=2|m+1|.
PC×OB=2|m+1|.
当m![]() ﹣1时,S=2m+2,
﹣1时,S=2m+2,
当m<﹣1时,S=﹣2m﹣2,
即△ABP的面积S=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目