题目内容
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作ABDE,连接AD、EC. 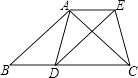
(1)试说明:△ADC≌△ECD;
(2)若BD=CD,试说明:四边形ADCE是矩形.
【答案】
(1)证明:∵AB=AC,
∴∠B=∠ACB,
又∵ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中,
 ,
,
∴△ADC≌△ECD(SAS).
(2)解:∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
【解析】(1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目