题目内容
【题目】在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是以点A为圆心4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为 ．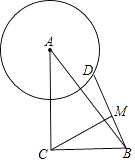 
【答案】7
【解析】解：作AB的中点E，连接EM、CE．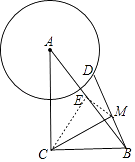 
在直角△ABC中，AB= 
= 
=10，
∵E是直角△ABC斜边AB上的中点，
∴CE= 
AB=5．
∵M是BD的中点，E是AB的中点，
∴ME= AD=2．
∴在△CEM中，5﹣2≤CM≤5+2，即2≤CM≤7．
∴最大值为7，
所以答案是：7．
【考点精析】利用直角三角形斜边上的中线和三角形中位线定理对题目进行判断即可得到答案，需要熟知直角三角形斜边上的中线等于斜边的一半；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：
A种产品 | B种产品 | |
成本（万元/件） | 2 | 5 |
利润（万元/件） | 1 | 3 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
