Question

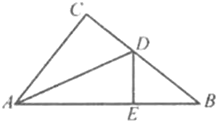
【题目】如图，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，交CB于点D，DE⊥AB，垂足为E，若AC=3，AB=5，则DE的长为______.

Answer 1

【答案】

【解析】

利用勾股定理求出BC的长，再利用角平分线的性质，易证CD=ED，利用HL证明Rt△ACD≌Rt△AED，根据全等三角形的对应边相等，可得AC=AE，即可求出BE的长，然后在Rt△BDE中，利用勾股定理求出DE的长.

解：在Rt△ABC中，，

∵AD平分∠CAB，DE⊥AB，∠ACB=90°，即AC⊥CB，

∴CD=DE，

在Rt△ACD和Rt△AED中，，

∴Rt△ACD≌Rt△AED(HL)，

∴AC=AE=3，

∴BE=AB-AE=5-3=2，

设DE=CD=x，则BD=4-x，

在Rt△BDE中，BD2=DE2+BE2，

∴(4-x)2=x2+4，

解得：，

∴，

故答案为：.