ƒøƒ⁄»ð
°æƒø°ø“—÷™≈◊ŒÔœþy£Ωx2+£®2m©Å1£©x©Å2m£®m£æ0.5£©µƒ◊ÓµÕµ„µƒ◊ð◊¯±ÍŒ™©Å4£Æ

£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
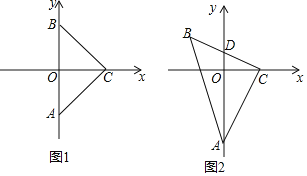
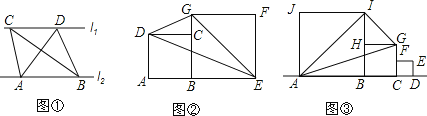
£®2£©»ÁÕº1£¨≈◊ŒÔœþ”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨DŒ™≈◊ŒÔœþ…œµƒ“ªµ„£¨BD∆Ω∑÷Àƒ±þ–ŒABCDµƒ√ʪ˝£¨«Ûµ„Dµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨∆Ω“∆≈◊ŒÔœþy£Ωx2+£®2m©Å1£©x©Å2m£¨ π∆‰∂•µ„Œ™◊¯±Í‘≠µ„£¨÷±œþy£Ω©Å2…œ”–“ª∂ص„P£¨π˝µ„P◊˜¡ΩÃı÷±œþ£¨∑÷±”Î≈◊ŒÔœþ”–Œ®“ªµƒπ´π≤µ„E°¢F£®÷±œþPE°¢PF≤ª”Îy÷·∆Ω––£©£¨«Û÷§£∫÷±œþEF∫„π˝ƒ≥“ª∂®µ„£Æ
°æ¥∞∏°ø£®1£©y£Ωx2+2x©Å3£ª£®2£©D£®©Å![]() £¨©Å
£¨©Å![]() £©£ª£®3£©º˚Ω‚Œˆ
£©£ª£®3£©º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©œ»«Û≥ˆ∂•µ„◊¯±Í£¨”…◊ÓµÕµ„µƒ◊ð◊¯±ÍŒ™©Å4£¨ø…¡–∑Ω≥㨺¥ø…«ÛΩ‚£ª
£®2£©¡¨ACΩªBD”⁄E£¨π˝A◊˜AM°ÕBD”⁄M£¨π˝C◊˜CN°ÕBD”⁄N£¨”…»˝Ω«–Œ√ʪ˝πÿœµ∫Õ»´µ»»˝Ω«–Œµƒ–‘÷ ø…«Ûµ„E◊¯±Í£¨ø…«ÛBDΩ‚Œˆ Ω£¨º¥ø…«Ûµ„D◊¯±Í£ª
£®3£©…ËE£®t£¨t2£©£¨F£®n£¨n2£©£¨ø…«ÛPEΩ‚Œˆ Ω£¨”…”Î≈◊ŒÔœþ”–Œ®“ªµƒπ´π≤µ„£¨ø…«Ûk1£Ω2t£¨º¥ø…«Ûµ„P∫·◊¯±Í£¨ø…µ√tn£Ω©Å2£¨…Ë÷±œþEFµƒΩ‚Œˆ ΩŒ™y£Ωkx+b£¨µ√x2©Åkx©Åb£Ω0£¨ø…«Ûb£Ω2£¨º¥ø…µ√÷±œþEF∫„π˝∂®µ„£®0£¨2£©£Æ
Ω‚£∫£®1£©°þy£Ωx2+£®2m©Å1£©x©Å2m£Ω£®x+m©Å0.5£©2©Åm2©Åm©Å0.25£¨
°ý∂•µ„◊¯±ÍŒ™£®0.5©Åm£¨©Åm2©Åm©Å0.25£©
°þ◊ÓµÕµ„µƒ◊ð◊¯±ÍŒ™©Å4£¨
°ý©Åm2©Åm©Å0.25£Ω©Å4£¨º¥4m2+4m©Å15£Ω0£¨
°ým£Ω1.5ªÚ©Å2.5£¨
°þm£æ0.5£¨°ým£Ω1.5£Æ
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y£Ωx2+2x©Å3£ª
£®2£©°þy£Ωx2+2x©Å3”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨
°ýA£®©Å3£¨0£©£¨B£®1£¨0£©£¨C£®0£¨©Å3£©£Æ
»ÁÕº£¨¡¨ACΩªBD”⁄E£¨π˝A◊˜AM°ÕBD”⁄M£¨π˝C◊˜CN°ÕBD”⁄N£¨
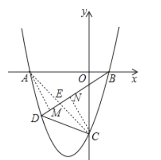
°þBD∆Ω∑÷Àƒ±þ–ŒABCDµƒ√ʪ˝£¨
°ýS°˜ABD£ΩS°˜CBD£¨
°ý![]() BD°¡AM£Ω
BD°¡AM£Ω![]() BD°¡CN£¨
BD°¡CN£¨
°ýAM£ΩCN£¨«“°œAEM£Ω°œCMN£¨°œAME£Ω°œCNE£Ω90°„
°ý°˜AEM°’°˜CEN£®AAS£©£¨
°ýAE£ΩCE£¨
°ýE£®©Å1.5£¨©Å1.5£©£¨«“B£®1£¨0£©£¨
°ý÷±œþBEµƒΩ‚Œˆ ΩŒ™y£Ω0.6x©Å0.6£Æ
°ý0.6x©Å0.6£Ωx2+2x©Å3£¨
Ω‚µ√x1£Ω©Å![]() £¨x2£Ω1£¨
£¨x2£Ω1£¨
°ýD£®©Å![]() £¨©Å
£¨©Å![]() £©£Æ
£©£Æ
£®3£©”…“‚ø…µ√∆Ω“∆∫ÛΩ‚Œˆ ΩŒ™y£Ωx2£¨
…ËE£®t£¨t2£©£¨F£®n£¨n2£©£¨
…Ë÷±œþPEŒ™y£Ωk1£®x©Åt£©+t2£¨
”…“‚ø…µ√ x2©Åk1x+k1t©Åt2£Ω0£¨
°ý°˜£Ωk12©Å4£®k1t©Åt2£©£Ω£®k1©Å2t£©2£Ω0£¨
°ýk1£Ω2t£Æ
°ý÷±œþPEŒ™y£Ω2t£®x©Åt£©+t2£¨º¥y£Ω2tx©Åt2£Æ
¡Óy£Ω©Å2£¨µ√xP£Ω![]() £¨
£¨
Õ¨¿Ì£¨…Ë÷±œþPFŒ™y£Ωk2£®x©Ån£©+n2£¨
°ýxP£Ω![]() £¨
£¨
°ý![]() £Ω
£Ω![]() £¨
£¨
°þt°Ÿn£¨
°ýtn£Ω©Å2£Æ
…Ë÷±œþEFµƒΩ‚Œˆ ΩŒ™y£Ωkx+b£¨µ√x2©Åkx©Åb£Ω0£¨
°ýxExF£Ω©Åb£¨º¥tn£Ω©Åb£¨
°ýb£Ω2£Æ
°ý÷±œþEFŒ™y£Ωkx+2£¨π˝∂®µ„£®0£¨2£©£Æ

°æƒø°øƒ≥–£—ß…˙ª·◊º±∏µ˜≤È¡˘ƒÍº∂—ß…˙≤Œº”°∞Œ‰ ı¿ý°±°¢°∞ Ȫ≠¿ý°±°¢°∞∆Â≈∆¿ý°±°¢°∞∆˜¿÷¿ý°±Àƒ¿ý–£±æøŒ≥õƒ»À ˝£Æ
£®1£©»∑∂®µ˜≤È∑Ω Ω ±£¨º◊Õ¨—ßÀµ£∫°∞Œ“µΩ¡˘ƒÍº∂£®1£©∞ý»•µ˜≤È»´ÃÂÕ¨—ß°±£ª““Õ¨—ßÀµ£∫°∞∑≈—ß ±Œ“µΩ–£√≈ø⁄Àʪ˙µ˜≤È≤ø∑÷Õ¨—ß°±£ª±˚Õ¨—ßÀµ£∫°∞Œ“µΩ¡˘ƒÍº∂√ø∏ˆ∞ýÀʪ˙µ˜≤È“ª∂® ˝¡øµƒÕ¨—ß°±£Æ«Î÷∏≥ˆƒƒŒªÕ¨—ßµƒµ˜≤È∑Ω Ω◊Ó∫œ¿Ì£Æ
¿ý± | ∆µ ˝£®»À ˝£© | ∆µ¬ |
Œ‰ ı¿ý | 0.25 | |
Ȫ≠¿ý | 20 | 0.20 |
∆Â≈∆¿ý | 15 | b |
∆˜¿÷¿ý | ||
∫œº∆ | a | 1.00 |
£®2£©À˚√«≤…”√¡À◊ÓŒ™∫œ¿Ìµƒµ˜≤È∑Ω∑® ’ºØ ˝æð£¨≤¢ªÊ÷∆¡À»ÁÕºÀ˘ 浃Õ≥º∆±Ì∫Õ…»–ŒÕ≥º∆Õº£Æ
«Îƒ„∏˘æð“‘…œÕº±ÌÃ·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
¢Ÿa=_____£¨b=_____£ª
¢⁄‘⁄…»–ŒÕ≥º∆Õº÷–£¨∆˜¿÷¿ýÀ˘∂‘”¶…»–Œµƒ‘≤–ƒΩ«µƒ∂» ˝ «_____£ª
¢€»Ù∏√–£¡˘ƒÍº∂”–—ß…˙560»À£¨«Îƒ„π¿º∆¥Û‘º”–∂ý…Ÿ—ß…˙≤Œº”Œ‰ ı¿ý–£±æøŒ≥ãÆ