Question

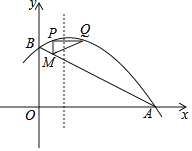
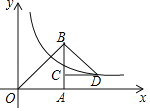
【题目】如图，在平面直角坐标系中，点B在函数y＝x图象上，点A在x轴的正半轴上，等腰直角三角形BCD的顶点C在AB上，点D在函数y＝第一象限的图象上若△OAB与△BCD面积的差为2，则k的值为（　　）

A.8B.4C.2D.1

Answer 1

【答案】B

【解析】

根据一次函数图象上点的坐标特征得出OA＝AB，由△BCD是等腰直角三角形，可得CD＝BD．设OA＝a，CD＝b，则点D的坐标为（a+b，a﹣b），根据反比例函数y＝的图象经过点D，即可得到a2﹣b2＝k，进而得出△OAB与△BCD的面积之差＝a2﹣b2＝k＝2，即可求出k．

解：∵点B在函数y＝x图象上，

∴OA＝AB，

∵△BCD是等腰直角三角形，

∴CD＝BD．

设OA＝a，CD＝b，则点D的坐标为（a+b，a﹣b），

∵反比例函数y＝的图象经过点D，

∴（a+b）（a﹣b）＝a2﹣b2＝k，

∴△OAB与△BCD的面积之差＝a2﹣b2＝k＝2，

∴k＝4，

故选：B．