Question

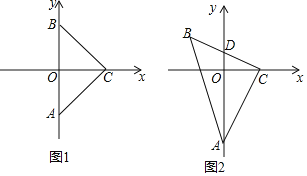
【题目】如图，△ABC在平面直角坐标系中，∠ACB＝90°，AC＝BC，A的坐标是（0，m）（m＜0），点C的坐标是（2，0），点B在x轴上方．

（1）如图1所示，若点B在y轴上，则m的值是　 　；

（2）如图2所示，BC与y轴交于点D．

①若m＝﹣6，求点B的坐标；

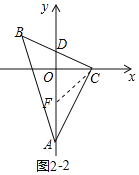
②若y轴恰好平分∠BAC，求OD的长．

Answer 1

【答案】（1）-2；（2）①B（﹣4，2）；②OD＝2﹣2．

【解析】

（1）利用等腰直角三角形的性质和判定解答即可；

（2）①如图2﹣1中，作BH⊥x轴于H．利用余角的性质可得∠BCH＝∠OAC，然后根据AAS即可证明△BHC≌△COA，进一步利用全等三角形的性质即可求出结果；

②如图2﹣2中，在OA截取一点F，使得OF＝OC，则OF和FC可得，由角平分线的性质和三角形的外角性质可得△AFC是等腰三角形，于是OA可得，易证△COD∽△AOC，然后利用相似三角形的性质即可求出结果．

解：（1）如图1中，∵CB＝CA，OC⊥AB，∴∠OCB＝∠OCA＝45°，

∴OA＝OC＝2，∴A（0，﹣2），∴m＝﹣2．

故答案为﹣2；

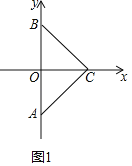
（2）①如图2﹣1中，作BH⊥x轴于H．

∵∠AOC＝∠BHC＝∠ACB＝90°，

∴∠BCH+∠ACO＝90°，∠ACO+∠OAC＝90°，

∴∠BCH＝∠OAC，

∵BC＝AC，∴△BHC≌△COA（AAS），

∴BH＝OC＝2，CH＝OA＝6，

∴OH＝CH﹣OC＝4，

∴B（﹣4，2）；

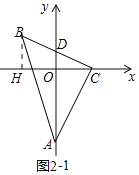
②如图2﹣2中，在OA截取一点F，使得OF＝OC．

∵OF＝OC＝2，∠FOC＝90°，∴FC＝2，∠OFC＝∠OCF＝45°，

∵AD平分∠CAB，∴∠DAC＝∠CAB＝22.5°，

∵∠OFC＝∠FAC+∠FCA，∴∠FCA＝22.5°，

∴∠FAC＝∠FCA＝22.5°，

∴AF＝CF＝2，

∴OA＝2+2，∴A（0，﹣2﹣2），

∵∠DCO＝∠OAC，∠COD＝∠AOC＝90°，

∴△COD∽△AOC，∴，即，

∴OD＝2﹣2．