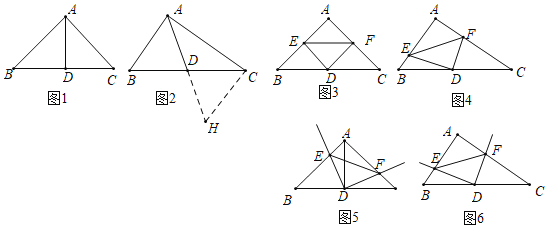
题目内容
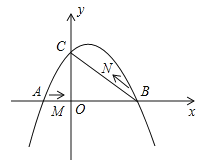
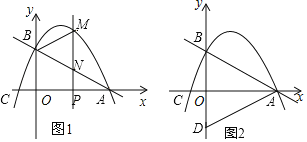
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0)和点C,与y轴交于点B.
(1)求抛物线解析式和点B坐标;
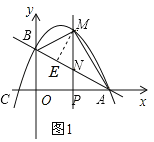
(2)在x轴上有一动点P(m,0)过点P作x轴的垂线交直线AB于点N,交抛物线与点M,当点M位于第一象限图象上,连接AM,BM,求△ABM面积的最大值及此时M点的坐标;
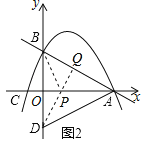
(3)如图2,点B关于x轴的对称点为D,连接AD,BC.
①填空:点P是线段AC上一点(不与点A、C重合),点Q是线段AB上一点(不与点A、B重合),则两条线段之和PQ+BP的最小值为 ;
②填空:将△ABC绕点A逆时针旋转a(0°<α<180°),当点C的对应点C′落在△ABD的边所在直线上时,则此时点B的对应点B′的坐标为 .
【答案】(1)抛物线解析式为y=![]() x2+
x2+![]() x+2,B(0,2);(2)S△ABM的最大值=4,(2,3);(3)
x+2,B(0,2);(2)S△ABM的最大值=4,(2,3);(3)![]() 或
或![]() 或
或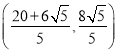 .
.
【解析】
(1)将A(4,0)代入y=ax2+(a+2)x+2,可求出a的值,将a的值代入即得到抛物线解析式,令x=0,求y,得点B坐标;
(2)待定系数法求直线AB的解析式,设点P(m,0),将S△ABM表示成m的二次函数,配方成顶点式即可求得△ABM面积的最大值及此时M点的坐标;
(3)①求PQ+BP的最小值利用对称进行转化,应用“两点之间线段最短”及“垂线段最短”可以得到“PQ+BP的最小值”即为点D到直线AB的距离;.
②题在△ABC绕A逆时针旋转过程中,按照依次落在直线BD、AD、AB上分类讨论.
(1)将A(4,0)代入y=ax2+(a+2)x+2,
得16a+4(a+2)+2=0,解得a=![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+2,
x+2,
令x=0,得y=2,
∴B(0,2);
(2)如图1,过点M作ME⊥AB于E,设P(m,0),M(m,![]() m2+
m2+![]() m+2),
m+2),
设直线AB的解析式为y=kx+b,将A(4,0),B(0,2)分别代入,
得![]() ,解得
,解得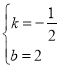 ,
,
∴直线AB的解析式为y=![]() x+2,
x+2,
∴N(m,![]() m+2),
m+2),
∴MN=![]() m2+
m2+![]() m+2-(
m+2-(![]() m+2)=
m+2)= ![]() m2+2m,
m2+2m,
∵MN⊥x轴,
∴MN∥y轴,
∴∠MNE=∠ABO,又∵∠MEN=∠AOB=90°,
∴△MEN∽△AOB,
∴![]() ,
,
∴ME×AB=AO×MN,
∴![]() =﹣(m﹣2)2+4,
=﹣(m﹣2)2+4,
∵﹣1<0,0<m<4,
∴当m=2时,S△ABM的最大值=4,
此时,点M的坐标为(2,3);
(3)①如图2,连接BP、DP、PQ,则PQ+BP=PQ+DP,只有当D、P、Q三点在同一直线上,且DP⊥AB时,PQ+BP的值最小.
过点D作DQ⊥AB于Q,交x轴于P,OA=4,OB=2,AB=![]() =2
=2![]() ,
,
∵B、D关于x轴对称,
∴D(0,﹣2),BD=4,
∵BD×AO=DQ×AB,
∴DQ=![]() ,即PQ+BP的最小值=
,即PQ+BP的最小值=![]() ,
,
故答案为:![]() ;
;
②如图3,点C′落在直线BD上,
在抛物线解析式y=![]() x2+
x2+![]() x+2中,令y=0,解得x1=4,x2=﹣1,
x+2中,令y=0,解得x1=4,x2=﹣1,
∴C(﹣1,0),AC=5,BC=![]() ,
,
∵AB2+BC2=(2![]() )2+(
)2+(![]() )2=25=AC2,
)2=25=AC2,
∴∠ABC=90°,
由旋转知,AC′=AC=5,B′C′=BC=![]() ,AB′=AB=2
,AB′=AB=2![]() ,∠AB′C′=∠ABC=90°,
,∠AB′C′=∠ABC=90°,
OC′=![]() =3,∴C′(0,﹣3),
=3,∴C′(0,﹣3),
设AB′交y轴于F,过B′作B′G⊥y轴于G,
∵∠AOF=∠C′B′F=90°,∠AFO=∠C′FB′
∴△AFO∽△C′FB′,
∴∠FAO=∠FC′B′,![]() ,即
,即![]() ,
,
∴AF=![]() ,
,
∵AO2+OF2=AF2,
∴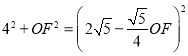 ,解得OF=
,解得OF=![]() ,
,
∴AF=![]() ,
,
∵∠C′GB′=∠AOF=90°,
∴△C′GB′∽△AOF,
∴![]() ,即B′G×AF=OF×B′C′,
,即B′G×AF=OF×B′C′,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即C′G×AF=OA×B′C′,
,即C′G×AF=OA×B′C′,
∴![]() ,∴
,∴![]() ,
,
∴![]() ;
;
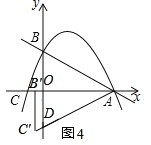
如图4,点C′落在直线AD上,∵∠BAC=∠OAD,
∴点B的对应点B′落在x轴上,由旋转知:△AB′C′≌△ABC,
∴AB′=AB=2![]() ,OB′=2
,OB′=2![]() -4,
-4,
∴B′(4-2![]() ,0);
,0);
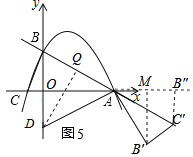
如图5,点C′落在直线AB上,过C′作C′B″⊥x轴于B″,作B′M⊥x轴于M,作DQ⊥AB于Q,
∵∠B″AC′=∠BAC=∠B′AC′,∠AB″C′=∠AB′C′=∠ABC=∠AQD=∠AM′=90°,AC′=AC=5,
∴∠BAD=∠B′AB″,AB=AD=AB′=AB″,
∴△ADQ≌△AB′M,
∴B′M=DQ=![]() ,
,
∴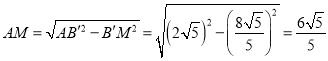 ,
,
OM=OA+AM=4+![]() =
=![]() ,
,
∴B′(![]() ,-
,-![]() ),
),
故答案为:![]() 或
或![]() 或
或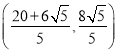 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案