题目内容
【题目】某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植﹣亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数y（亩）与补贴数额x（元）之间大致满足如图1所示的一次函数关系．随着补贴数额x的不断增大，出口量也不断增加，但每亩蔬菜的收益z（元）会相应降低，且z与x之间也大致满足如图2所示的一次函数关系．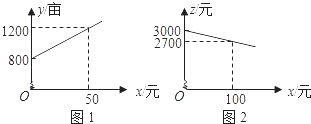 
（1）在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？
（2）分别求出政府补贴政策实施后，种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式；
（3）要使全市这种蔬菜的总收益w（元）最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值．
【答案】
（1）解：政府没出台补贴政策前，这种蔬菜的收益额为3000×800=2400000（元）
（2）解：设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为：
y=kx+800，z=k1x+3000，
分别把点（50，1200），（100，2700）代入得，
50k+800=1200，100k1+3000=2700，
解得：k=8，k1=﹣3，
种植亩数与政府补贴的函数关系为：y=8x+800
每亩蔬菜的收益与政府补贴的函数关系为z=﹣3x+3000（x＞0）
（3）解：由题意：
w=yz=（8x+800）（﹣3x+3000）
=﹣24x2+21600x+2400000
=﹣24（x﹣450）2+7260000，
∴当x=450，即政府每亩补贴450元时，总收益额最大，为7260000元
【解析】（1）根据题意可知直接计算这种蔬菜的收益额为3000×800=2400000（元）；（2）设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为：y=kx+800，z=k1x+3000，并根据图象上点的坐标利用待定系数法求函数的解析式即可；（3）表示出蔬菜的总收益w（元）与x之间的关系式，w=﹣24x2+21600x+2400000，利用二次函数最值问题求最大值．
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全下表：
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
（2）填空：
由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把菱形的面积S记为S(α)．例如：当α＝30°时，
；当α＝135°时，
．由上表可以得到
( ______°)；
( ______°)，…，由此可以归纳出
．
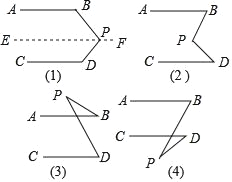
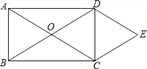
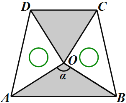
（3） 两块相同的等腰直角三角板按如图的方式放置，AD＝
，∠AOB＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干（它们除颜色外都相同），现随机从中摸出10枚记下颜色后放回，这样连续做了10次，记录了如下的数据：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据，解答下列问题：
（I）直接填空：第10次摸棋子摸到黑棋子的频率为 ；
（Ⅱ）试估算袋中的白棋子数量．
