题目内容
【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数
的图象与性质．列表：
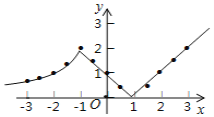
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．
如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
研究函数并结合图象与表格，回答下列问题：
点
，
，
，
在函数图象上，则
______
，
______
；
填“
”，“
”或“
”
当函数值
时，求自变量x的值；
在直线
的右侧的函数图象上有两个不同的点
，
，且
，求
的值；
若直线
与函数图象有三个不同的交点，求a的取值范围．
【答案】（1）见解析；（2）①
，；②x=3或x=-1；③2；④
【解析】
（1）根据函数图像的画法，从左至右依次连接个点，即可解决；
（2）①根据A点与B点的横坐标，判断两点所在的函数图像，然后根据函数的性质解决即可；根据C点与D点的纵坐标，判断两点所在的函数图像，然后结合函数图像解决即可.
②当
时，判断其所在的函数图像，然后结合函数解析式计算解决即可.③由图可知
时，所以两点在函数
的图像上，然后根据函数的对称性解决即可.④结合函数图像，
与函数图象有三个不同的交点，可知必须与两函数图像分别相交才可以，据此解决即可；
解：
如图所示：
，
，
A与B在
上，y随x的增大而增大，
；
，
，
C与D在上，观察图象可得
；
②当时，
，
不符合
；
当时，
，
或
；
，
在的右侧，
时，点关于
对称，
，
；
④由图象可知，当与分段函数分别相交时才会有三个不同的交点，观察函数图像y＞0，且y＜2，故a的取值范围为.
练习册系列答案
相关题目
