Question

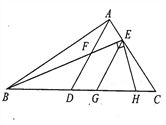
【题目】如图17－Z－12所示，等腰三角形ABC的底边长为8 cm，腰长为5 cm，一动点P在底边上从点B向点C以0.25 cm/s的速度移动，请你探究：当点P运动几秒时，点P与顶点A的连线AP与腰垂直？

图17－Z－12

Answer 1

【答案】当点P运动7 s或25 s时，点P与顶点A的连线AP与腰垂直

【解析】试题分析：分类讨论，AP分别与两个腰垂直，利用勾股定理计算时间.

应分两种情况：

(1)设当点P运动t(0≤t≤32)s时，AP与腰AC垂直，过点A作AD⊥BC，垂足为D，如图①所示．因为△ABC为等腰三角形，所以D为BC的中点，则BD＝CD＝4 cm，根据勾股定理得AD＝3 cm.在Rt△ACP中，AP2＝CP2－AC2＝(8－0.25t)2－52，在Rt△ADP中，AP2＝AD2＋DP2＝32＋(4－0.25t)2，所以(8－0.25t)2－52＝32＋(4－0.25t)2，解得t＝7.因此当23点P运动7 s时，AP与腰AC垂直．

(2)设当点P运动t(0≤t≤32)s时，AP与腰AB垂直，过点A作AD⊥BC，垂足为D，如图②所示．因为△ABC为等腰三角形，所以D为BC的中点，则BD＝CD＝4 cm，根据勾股定理得AD＝3 cm.在Rt△ABP中，AP2＝BP2－AB2＝(0.25t)2－52，在Rt△ADP中，AP2＝AD2＋DP2＝32＋(0.25t－4)2，所以(0.25t)2－52＝32＋(0.25t－4)2，解得t＝25.因此当点P运动25 s时，AP与腰AB垂直．

综上，当点P运动7 s或25 s时，点P与顶点A的连线AP与腰垂直