题目内容
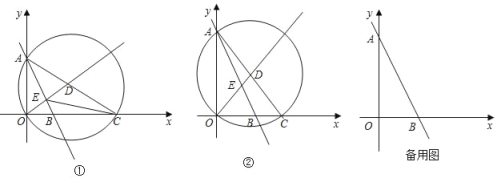
【题目】如图,在平面直角坐标系中,直线y=﹣2x+4与坐标轴交于A,B两点,动点C在x轴正半轴上,⊙D为△AOC的外接圆,射线OD与直线AB交于点E.
(1)如图①,若OE=DE,求![]() 的值;
的值;
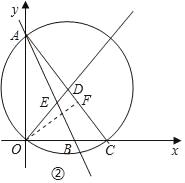
(2)如图②,当∠ABC=2∠ACB时,求OC的长;
(3)点C由原点向x轴正半轴运动过程中,设OC的长为a,
①用含a的代数式表示点E的横坐标xE;②若xE=BC,求a的值.
【答案】(1)![]() ;(2)OC=2
;(2)OC=2![]() ﹣2;(3)①xE=
﹣2;(3)①xE=![]() ;②a的值为
;②a的值为![]() ±1.
±1.
【解析】
(1)根据三角形的面积公式计算;
(2)作OF⊥AC于点F,根据一次函数的性质求出OA、OB,根据正切的定义得到tan∠ODC=2,设DF=m,根据勾股定理用m表示出OD,计算即可;
(3)①作EH⊥AO于点H,根据相似三角形的性质列式计算,得到答案;
②分C在点B右侧、C在点B左侧两种情况,分别列出方程,解方程即可.
(1)∵OE=DE,
∴S△AOE=S△ADE,
∵AD=CD,
∴S△CDE=S△ADE,
∴![]() ,
,
故答案为:![]() ;
;
(2)作OF⊥AC于点F,
对于直线y=﹣2x+4,当y=0时,x=2,当x=0时,y=4,
则A的坐标为(0,4),点B的坐标为(2,0),即OA=4,OB=2,
∵∠ABC=2∠ACB,
∴∠ADO=∠ABC,
∴∠ODC=∠ABO,
∴tan∠ODC=tan∠ABO=2,
设DF=m,则OF=2m,
由勾股定理得,OD=![]() m,
m,
∴CF=(![]() ﹣1)m,
﹣1)m,
∴tan∠OCD=![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,OC=2![]() ﹣2;
﹣2;
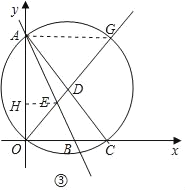
(3)①设直线OD交⊙D另一点为G,连结AG,作EH⊥AO于点H,
则EH∥AG,
∴![]() ,
,![]() ,
,
∴![]() =1,即
=1,即![]() =1,
=1,
解得,xE=![]() ;
;
②当C在点B右侧时,BC=xE,即a﹣2=xE,
∴a﹣2=![]() ,
,
解得,a1=1+![]() ,a2=1﹣
,a2=1﹣![]() (舍去),
(舍去),
当C在点B左侧时,BC=xE,即2﹣a=xE,
∴2﹣a=![]() ,
,
解得,a1=﹣1+![]() ,a2=﹣1﹣
,a2=﹣1﹣![]() (舍去),
(舍去),
所以a的值为![]() ±1.
±1.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()