题目内容
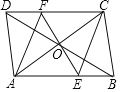
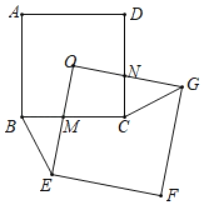
【题目】如图,已知正方形OEFG的顶点O与正方形ABCD的中心O重合,若正方形OEFG绕O点旋转.
(1)探究:在旋转的过程中线段BE与线段CG有什么数量关系及位置关系?证明你的结论;
(2)若正方形ABCD的边长为a,探究:在旋转过程中四边形OMCN的面积是否发生变化?若不变化求其面积,若变化指出变化过程.
【答案】(1)BE=CG,BE⊥CG,理由见解析;(2)不发生变化,![]() a2.
a2.
【解析】
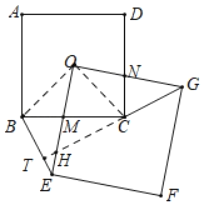
(1)连接OB、OC,延长GC交BE于T点,交OE于H点,根据四边形ABCD、EFGO是正方形,可以得到OG=OE,OB=OC,∠EOB=∠GOC,则△OBE≌△OCG,得到BE=CG,利用对顶角和等量代换可得到∠THE=90°,即BE⊥CG;
(2)利用ASA定理证明△OBM≌△OCN,得到S△OCN=S△OBM,则四边形OMCN和面积等于△BOC的面积,则无论怎么旋转OMCN的面积都是不变的.
解:(1)BE=CG,BE⊥CG,理由如下:
连接OB、OC,延长GC交BE于T点,交OE于H点,
∵O是正方形的中心,∴OB=OC.
∵∠BOE+∠MOC=90°,∠COG+∠MOC=90°,
∴∠BOE=∠COG.
又OE=OG,
∴△OBE≌△OCG(SAS).
∴BE=CG,∠BEO=∠CGO.
∵∠OHG+∠CGO=90°,∠OHG=∠EHT,
∴∠EHT+∠BEO=90°,即∠HTE=90°,
所以GC⊥BE.
(2)在旋转过程中四边形OMCN的面积不发生变化,理由如下:
在△OBM和△OCN中
![]()
∴△OBM≌△OCN(ASA)
∴四边形OMCN的面积=△OMC面积+△OCN面积=△OMC面积+△OBM面积=△OBC面积.
∵△OBC面积=![]() a2.
a2.
所以在旋转过程中四边形OMCN的面积不发生变化.
故答案为:(1)BE=CG,BE⊥CG,理由见解析;(2)不发生变化,![]() a2.
a2.