题目内容
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
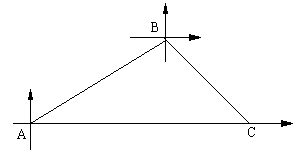
(1)港口A与小岛C之间的距离
(2)甲轮船后来的速度.

(1)港口A与小岛C之间的距离
(2)甲轮船后来的速度.
(1)A、C间的距离为(15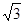 +15)海里 (2)5
+15)海里 (2)5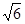 海里/小时
海里/小时
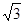 +15)海里 (2)5
+15)海里 (2)5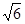 海里/小时
海里/小时试题分析:(1)作BD⊥AC于点D
由题意可知:AB=30×1=30,∠BAC=30°,∠BCA=45°
在Rt△ABD中
∵AB=30,∠BAC=30°
∴BD=15,AD=ABcos30°=15
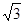
在Rt△BCD中,
∵BD=15,∠BCD=45°
∴CD=15,BC=15
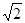
∴AC=AD+CD=15
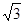 +15
+15即A、C间的距离为(15
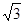 +15)海里 6分
+15)海里 6分(2)∵AC=15
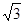 +15
+15轮船乙从A到C的时间为
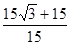 =
=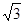 +1
+1由B到C的时间为
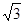 +1-1=
+1-1=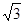
∵BC=15
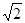
∴轮船甲从B到C的速度为
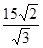 =5
=5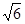 (海里/小时)
(海里/小时)答:轮船甲从B到C的速度为5
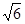 海里/小时
海里/小时 点评:本题考查解三角形,掌握三角函数和勾股定理的内容,并运用它们来解题

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
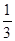 ,则tanA=
,则tanA=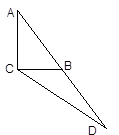
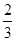
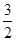

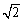 海里
海里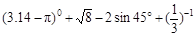 .
. 中,
中,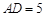 ,
,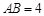 ,
,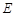 是
是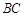 上的一点,
上的一点,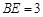 ,
,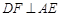 ,垂足为
,垂足为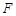 ,则
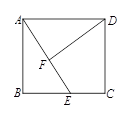
,则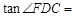 .
.
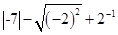 -
-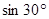
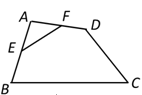
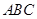 中,
中, ,
,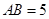 ,
, ,则
,则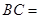 ,
,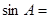 .
.