题目内容
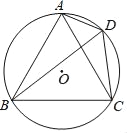
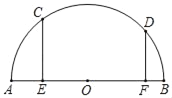
【题目】如图，AB是半圆O的直径，C、D两点在半圆上，CE⊥AB于E，DF⊥AB于F，点P是AB上的一个动点，已知AB=10，CE=4，DF=3，则PC+PD的最小值是（ ）
A. 7 B. 7
C. 10 D. 8
【答案】B
【解析】
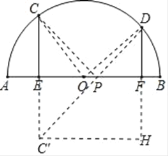
作点C关于AB的对称点C′，连接C′D交AB于点P，则此时PC+PD最小，为 C′D的长，求得C′D的长即可求得PC+PD的最小值.
解：作点C关于AB的对称点C′，连接C′D交AB于点P，
则此时PC+PD最小，
连接OC，OD，
由勾股定理得，OE=
=3，OF=4，
∴EF=EO+OF=7，
作C′H⊥DF交DF的延长线于H，
则四边形EC′HF为矩形，
∴FH=C′E=CE=4，C′H=EF=7，
∴DH=DF+FH=7，
∴PC+PD=C′D=
.
故选B．
练习册系列答案
相关题目
