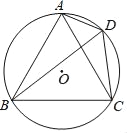
题目内容
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
【答案】(1)见解析;(2)四边形ABCD的面积为![]() .
.
【解析】
(1)据已知条件和圆周角定理即可得到结论;
(2)过点A作AE⊥CD,过点B作BF⊥AC,得∠AED=90°,∠ADE=60°,∠DAE=30°,DE =1,![]() ,CE= 5,从而求出
,CE= 5,从而求出![]() ,再求出
,再求出![]() ,即可求出结论.
,即可求出结论.
解:(1)∵ 四边形ABCD内接于⊙O
∴ ∠ABC+∠ADC=180°
∵ ∠ABC=60°,∴ ∠ADC=120°
∵ DB平分∠ADC,∴ ∠ADB=∠CDB=60°
∴ ∠ACB=∠ADB=60°,∠BAC=∠CDB=60°
∴ ∠ABC=∠BCA=∠BAC
∴ △ABC是等边三角形

⑵ 过点A作AE⊥CD,垂足为点E;
过点B作BF⊥AC,垂足为点F.
∴ ∠AED=90°
∵ ∠ADC=120° ∴ ∠ADE=60° ∴ ∠DAE=30°
∴ DE=![]() =1,
=1,![]()
∵ CD=4
∴ CE=CD+DE=1+4=5
∴ ![]()
Rt△AEC中,∠AED=90°
∴ AC=![]()
∵ △ABC是等边三角形
∴ AB=BC=AC=![]()
∴ AF=FC=![]()
∴![]()
∴![]()
∴ 四边形ABCD的面积=![]() .
.

练习册系列答案
相关题目