题目内容
【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
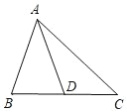
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
【答案】(1)详见解析;(2)A'B=AC;(3)AB+AC>2AD,理由详见解析.
【解析】
(1)作图;
(2)证明△ADC≌△A'DB,可知AC=A'B;
(3)根据三角形三边关系得:AB+BA'>AA',即AB+AC>AD+A'D,所以AB+AC>2AD.
(1)如图所示,延长 AD 至 A',使 AD=A'D,连接 A'B,则△A'DB 就是与△ACD 关于点 D 成中心对称的三角形;

(2)A'B=AC,
理由是:在△ADC 和△A'DB 中,
∵ ,
,
∴△ADC≌△A'DB(SAS),
∴AC=A'B;
(3)AB+AC>2AD;
理由:∵△ADC 与△A'DB 关于 D 点成中心对称,
∴AD=A'D,AC=A'B.
在△ABA'中,AB+BA'>AA', 即 AB+AC>AD+A'D.
∴AB+AC>2AD.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目