Question

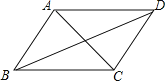
【题目】将两个全等的直角三角形和按图1方式摆放，其中 ，,点落在上，所在直线交所在直线于点.

(1)求的度数;

(2)求证: ;

(3)若将图1中绕点按顺时针方向旋转至如图2，其他条件不变，请你写出如图2中与之间的关系，并加以证明.

Answer 1

【答案】（1）∠CFE=120°；（2）见解析；（3）AF=DE+EF

【解析】

（1）由直角三角形的性质即可得出结果；

（2）连接BF，由SAS证明△BCF≌△BEF即可；

（3）由全等三角形的性质即可得出结论．

(1)∵∠ACB=∠DEB=90°,∠A=30°，

∴∠AEF=90°,∠AFE=90°30°=60°，

∴∠CFE=180°∠AFE=120°.

(2)证明：连接BF，如图1所示：

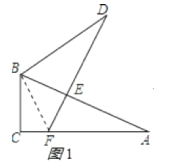
∵△DBE≌△ABC，

∴BE=BC，DE=AC.

在Rt△BCF和Rt△BEF中, ，

∴Rt△BCF≌Rt△BEF(HL)

∴CF=EF；

（3）DE+EF=AF，理由如下：

∵CF=EF，AC=DE，

∴DE+EF=AC+CF=AF.