ЬтФПФкШн
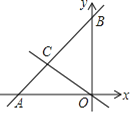
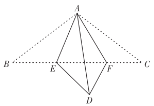
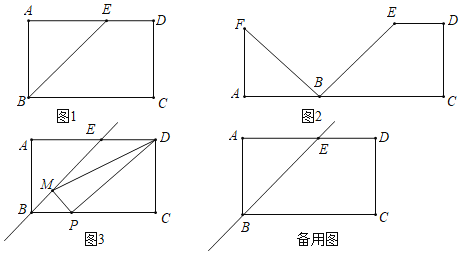
ЁОЬтФПЁПШч1ЃЌдкОиаЮABCDжаЃЌABЃН6ЃЌADЃН10ЃЌEЮЊADЩЯвЛЕуЧвAEЃН6ЃЌСЌНгBEЃЎ
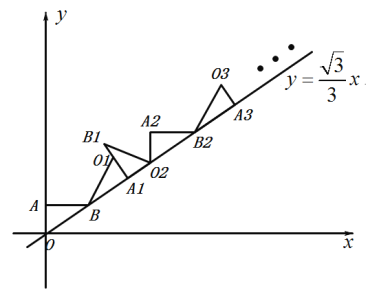
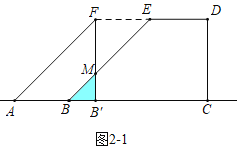
ЃЈ1ЃЉНЋЁїABEШЦЕуBФцЪБеыа§зЊ90ЁужСЁїABFЃЈШчЭМ2ЃЉЃЌЧвAЁЂBЁЂCШ§ЕуЙВЯпЃЌдйНЋЁїABFбиЩфЯпBCЗНЯђЦНвЦЃЌЦНвЦЫйЖШЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌЦНвЦЪБМфЮЊtЃЈsЃЉЃЈtЁн0ЃЉЃЌЕБЕуAгыЕуCжиКЯЪБдЫЖЏЭЃжЙЃЎ
ЂйдкЦНвЦЙ§ГЬжаЃЌЕБЕуFгыЕуEжиКЯЪБЃЌtЃНЁЁ ЁЁЃЈsЃЉЃЎ
ЂкдкЦНвЦЙ§ГЬжаЃЌЁїABFгыЫФБпаЮBCDEжиЕўВПЗжУцЛ§МЧЮЊSЃЌЧѓsгыtЕФЙиЯЕЪНЃЎ
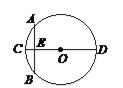
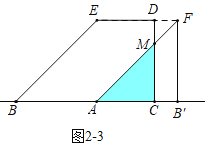
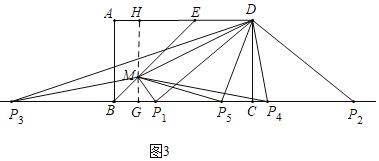
ЃЈ2ЃЉШчЭМ3ЃЌЕуMЮЊжБЯпBEЩЯвЛЕуЃЌжБЯпBCЩЯгавЛИіЖЏЕуPЃЌСЌНгDMЁЂPMЁЂDPЃЌЧвEMЃН5![]() ЃЌЪдЮЪЃКЪЧЗёДцдкЕуPЃЌЪЙЕУЁїDMPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіДЫЪБЯпЖЮBPЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌЪдЮЪЃКЪЧЗёДцдкЕуPЃЌЪЙЕУЁїDMPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіДЫЪБЯпЖЮBPЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй6ЃЛЂкSЃН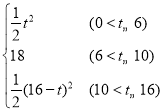 ЃЛ
ЃЛ
ЃЈ2ЃЉДцдкЃЌ 10Љ![]() Лђ10+
Лђ10+![]() Лђ
Лђ![]() Љ1Лђ
Љ1Лђ![]() +1Лђ
+1Лђ ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйШчЭМ1жаЃЌСЌНгEFЃЎЧѓГіEFЕФГЄМДПЩНтОіЮЪЬтЃЎ
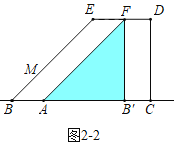
ЂкЗжШ§жжЧщаЮЃКШчЭМ2Љ1жаЃЌЕБ0ЃМtЁм6ЪБЃЌжиЕўВПЗжЪЧЁїBMBЁфЃЎШчЭМ2Љ2жаЃЌЕБ6ЃМtЁм10ЪБЃЌжиЕўВПЗжЪЧЁїAFBЁфЃЎШчЭМ2Љ3жаЃЌЕБ10ЃМtЁм16ЪБЃЌжиЕўВПЗжЪЧЁїAMCЃЌЗжБ№ЧѓНтМДПЩЃЎ
ЃЈ2ЃЉЗжШ§жжЧщаЮЃКDMЃНDPЃЌDMЃНPMЃЌPMЃНPDЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЂйШчЭМ1жаЃЌСЌНгEFЃЎ
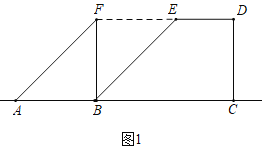
гЩЬтвтEFЃНABЃНBFЃН6ЃЌ
ЁрtЃН6ЪБЃЌЕуFгыЕуEжиКЯЃЌ
ЙЪД№АИЮЊ6ЃЎ
ЂкШчЭМ2Љ1жаЃЌЕБ0ЃМtЁм6ЪБЃЌжиЕўВПЗжЪЧЁїBMBЁфЃЌ
BBЁЏ=MBЁЏ=tЃЌ
SЃН![]() t2ЃЎ
t2ЃЎ
ШчЭМ2Љ2жаЃЌЕБ6ЃМtЁм10ЪБЃЌжиЕўВПЗжЪЧЁїAFBЁфЃЌ
ABЁЏ=FBЁЏ=6
SЃН![]() ЁС6ЁС6ЃН18ЃЎ
ЁС6ЁС6ЃН18ЃЎ
ШчЭМ2Љ3жаЃЌЕБ10ЃМtЁм16ЪБЃЌжиЕўВПЗжЪЧЁїAMCЃЌ
AC=MC=16-tЃЌ
SЃН![]() ЃЈ16ЉtЃЉ2ЃЌ
ЃЈ16ЉtЃЉ2ЃЌ
злЩЯЫљЪіЃЌSЃН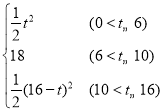 ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ3жаЃЌзмMHЁЭADгкHЃЌНЛBCгкGЃЎ
ЁпABЃНAEЃН6ЃЌЁЯAЃН90ЁуЃЌ
ЁрBEЃН6![]() ЃЌ
ЃЌ
ЁпEMЃН5![]() ЃЌ
ЃЌ
ЁрBMЃН![]() ЃЌ
ЃЌ
ЁрBGЃНMGЃНAHЃН1ЃЌHMЃНHEЃН5ЃЌDHЃНADЉAHЃН9ЃЌ
ЁрDMЃН![]() ЃЌ
ЃЌ
ЕБDMЃНDPЪБЃЌПЩЕУCP1ЃНCP2ЃН![]() ЃЌ
ЃЌ
ЁрBP1ЃН10Љ![]() ЃЌBP2ЃН10+
ЃЌBP2ЃН10+![]() ЃЎ
ЃЎ
ЕБMDЃНMPЪБЃЌПЩЕУGP3ЃНGP4ЃН![]() ЃЌ
ЃЌ
ЁрBP3ЃН![]() Љ1ЃЌBP4ЃН
Љ1ЃЌBP4ЃН![]() +1ЃЌ
+1ЃЌ
ЕБPMЃНPDЪБЃЌЩшGP5ЃНxЃЌдђ![]() ЃЌ
ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрBP5ЃН1+![]() ЃН
ЃН![]() ЃЎ
ЃЎ

 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИЁОЬтФПЁПбЇаЃЖдГѕ2021МЖМзЁЂввСНАрИї60УћбЇЩњНјаажЊЪЖВтЪдЃЈТњЗж60ЗжЃЉЃЌВтЪдЭъГЩКѓЗжБ№ГщШЁСЫ12ЗнГЩМЈЃЌећРэЗжЮіЙ§ГЬШчЯТЃЌЧыВЙГфЭъећ.
ЃЈЪеМЏЪ§ОнЃЉ
МзАр12УћбЇЩњВтЪдГЩМЈЭГМЦШчЯТЃК
45ЃЌ59ЃЌ60ЃЌ38ЃЌ57ЃЌ53ЃЌ52ЃЌ58ЃЌ60ЃЌ50ЃЌ43ЃЌ49
ввАр12УћбЇЩњВтЪдГЩМЈЭГМЦШчЯТЃК
35ЃЌ55ЃЌ46ЃЌ39ЃЌ54ЃЌ47ЃЌ43ЃЌ57ЃЌ42ЃЌ59ЃЌ60ЃЌ47
ЃЈећРэЪ§ОнЃЉ
АДШчЯТЗжЪ§ЖЮећРэЃЌУшЪіетСНзщбљБОЪ§Он
зщБ№ЦЕЪ§ |
|
|
|
|
|
Мз | 0 | 1 | 3 | 3 | 5 |
вв | 2 | 2 | 3 | 1 | 4 |
ЃЈЗжЮіЪ§ОнЃЉ
СНзщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§ЁЂжаЮЛЪ§ЁЂЗНВюШчЯТБэЫљЪОЃК
АрМЖ | ЦНОљЪ§ | жкЪ§ | жаЮЛЪ§ |
Мз |
| 52.5 | |
вв | 48.7 | 47 |
|
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЙцЖЈЕУЗждк40ЗжМАвдЩЯЮЊКЯИёЃЌЧыЙРМЦввАр60УћбЇЩњжажЊЪЖВтЪдКЯИёЕФбЇЩњгаЖрЩйШЫЃП
ЃЈ3ЃЉФуШЯЮЊФФИіАрЕФбЇЩњжЊЪЖВтЪдЕФећЬхЫЎЦННЯКУЃЌЧыЫЕУївЛЬѕРэгЩ.