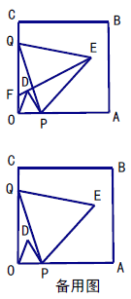
题目内容
【题目】如图,已知等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一个动点,将
上的一个动点,将![]() 沿着
沿着![]() 折叠到
折叠到![]() 处,再将边
处,再将边![]() 折叠到与
折叠到与![]() 重合,折痕为
重合,折痕为![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长是___________.
的长是___________.
【答案】![]() ,
,![]() ,
,![]()
【解析】
分三种情况:DE=DF,EF=ED,EF=FD,进行讨论即可.
解:由折叠可知:∠B=∠ADE, ∠C=∠ADF,AB=AD=5,AC=AD=5,BE=ED,DF=FC
过A作AM⊥BC于M

∵AB=AC
∴BM=CM=![]() BC=4,∠B=∠C
BC=4,∠B=∠C
∴∠B=∠ADE=∠C=∠ADF
由勾股定理可知:![]()
当DE=DF=a时,

则BE=ED=DF=FC=a,EM=BM-BE=4-x
∵∠ADE=∠ADF
∴AD⊥BC
又∵AM⊥BC
∴A、M、D三点共线,∠EMD=90°
∴DM=AD-AM=5-3=2
在Rt△EMD中:![]()
∴![]()
解得:![]()
当DE=EF时,
∵BE=ED
∴BE=EF
连接BD,延长AE交BD于G

∵AB=AD,BE=ED
∴AG垂直平分BD
∴BG=DG
设EM=b则BE=EF=4-b
∴FC=8-(8-2b)=2b
∴FD=FC=2b
在△BMD中: BG=DG,BE=EF
∴EG是△BMD的中位线
∴![]()
∴GE=EM=b
∵∠BME=∠AHE=90°,∠BEG=∠AEM
∴![]()
∴BG=AM=3
在Rt△BEG中:![]()
∴![]()
∴![]()
∴BE=4-![]()
当DF=EF时,
∵CF=DF
∴CF=EF
连接CD,延长AF交CD于H
∵AC=AD,DF=FC
∴AH垂直平分CD
∴DH=CH
设FM=c则FC=FD=4-c
∴BE=8-(8-2c)=2c
∴BE=ED=2c
在△ECD中: EF=FC,DH=HC
∴FH是△ECD的中位线
∴![]()
∴FH=FM=c

∵∠AMF=∠CHF=90°,∠AFM=∠CFH
∴![]()
∴CH=AM=3
在Rt△FCH中:![]()
∴![]()
∴![]()
∴BE=![]()
故答案为:![]() ,
,![]() ,
,![]()

练习册系列答案
相关题目