题目内容
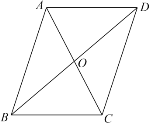
【题目】在一次数学活动中，老师准备三张完全相同的纸片，纸片上分别写有如图所示图形的一个条件：①AD＝BC；②AB∥DC；③AO=OC，小明同学从三张纸片中任意抽取两张．请你用树状图或表格表示出抽取两张纸片上的条件所有可能出现的结果（用序号表示），并求出上述条件下四边形ABCD是平行四边形的概率．
【答案】画图见解析；概率为
；
【解析】
先画树状图，再根据所得的结果，判断使四边形能构成平行四边形的概率．
解：抽取两张卡片上的等式的所有可能出现的结果为：
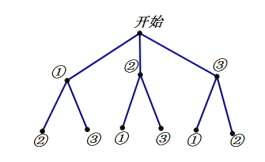
故可能发生的情况一共有6种，
根据平行四边形的判定定理，取到②③可以证明是平行四边形，理由如下：
∵AB∥DC，
∴
，
又∵
（对顶角相等），
且
,
∴
≌
（AAS），
∴
（全等三角形对应边相等），
∴四边形ABCD是平行四边形（一组对边分别平行且相等的四边形是平行四边形），
故概率为：
．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校为了解九年级学生每天参加体育锻炼额时间，从该校九年级学生中随机抽取20名学生进行调查，得到如下数据（单位：分钟）：
30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析，得到下列表一和表二：
表一
时间t（单位：分钟） |
|
|
|
|
人数 | 2 | a | 10 | b |
表二
平均数 | 中位数 | 众数 |
60 | c | d |
根据以上提供信息，解答下列问题：
（1）填空
①a= b=
②c= d=
（2）如果该校现有九年级学生200名，请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。
