Question

【题目】（问题情境）在△ABC中，BA＝BC，∠ABC＝α（0°＜α＜180°），点P为直线BC上一动点（不与点B、C重合），连接AP，将线段PA绕点P顺时针旋转得到线段PQ旋转角为α，连接CQ．

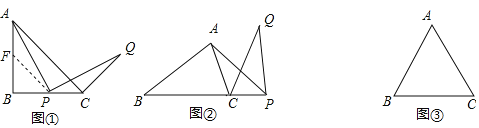
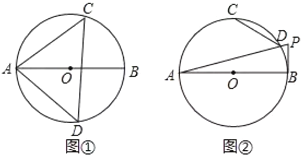
（特例分析）（1）当α＝90°，点P在线段BC上时，过P作PF∥AC交直线AB于点F，如图①，易得图中与△APF全等的一个三角形是　 ，∠ACQ＝　 　°．

（拓展探究）（2）当点P在BC延长线上，AB：AC＝m：n时，如图②，试求线段BP与CQ的比值；

（问题解决）（3）当点P在直线BC上，α＝60°，∠APB＝30°，CP＝4时，请直接写出线段CQ的长．

Answer 1

【答案】（1）△PQC，90；（2）；（3）线段CQ的长为2或8．

【解析】

（1）△ABC是等腰直角三角形，PF∥AC，得到△BPF是等腰直角三角形，证明AF＝CP，利用旋转的旋转证明AP＝PQ，∠PAF＝∠QPC，从而可得结论，

（2）过P作PF∥AC，交BA的延长线于F，则，再证明△AFP≌△PCQ，利用△ABC∽△FBP的性质可得答案，

（3）分情况讨论：当P在CB的延长线上时，证明△APC≌△QPC，利用等边三角形的性质可得答案，当P在BC的延长线上时，连接AQ，利用等边三角形的性质，证明△ACQ≌△PCQ，从而可得答案．

解：（1）如图①，∵∠ABC＝90°，AB＝CB，

∴△ABC是等腰直角三角形，

∵PF∥AC，

∴∠BPF＝∠BFP＝45°，

∴△BPF是等腰直角三角形，

∴BF＝BP，

∴AF＝CP，

由旋转可得，AP＝PQ，∠APQ＝90°，而∠BPF＝45°，

∴∠QPC＝45°﹣∠APF，

又∵∠PAF＝∠PFB﹣∠APF＝45°﹣∠APF，

∴∠PAF＝∠QPC，

∴△APF≌△PQC，

∴∠PCQ＝∠AFP＝135°，

又∵∠ACB＝45°，

∴∠ACQ＝90°，

故答案为：△PQC，90；

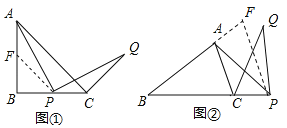
（2）如图②，过P作PF∥AC，交BA的延长线于F，则，

又∵AB＝BC，

∴AF＝CP，

又∵∠FAP＝∠ABC+∠APB＝α+∠APB，∠CPQ＝∠APQ+∠APB＝α+∠APB，

∴∠FAP＝∠CPQ，

由旋转可得，PA＝PQ，

∴△AFP≌△PCQ，

∴FP＝CQ，

∵PF∥AC，

∴△ABC∽△FBP，

∴，

∴

（3）如图，当P在CB的延长线上时，

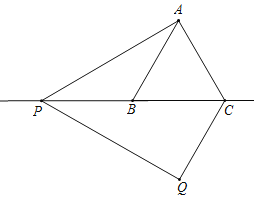
∠CPQ＝∠APQ﹣∠APB＝60°﹣30°＝30°，

∴∠APC＝∠QPC，

又∵AP＝QP，PC＝PC，

∴△APC≌△QPC，

∴CQ＝AC，

又∵BA＝BC，∠ABC＝60°，

∴△ABC是等边三角形，

∴∠ABC＝60°，∠BAP＝∠ABC﹣∠APB＝30°，

∴BP＝AB＝BC＝PC＝2，

∴QC＝AC＝BC＝2；

如图，当P在BC的延长线上时，连接AQ，

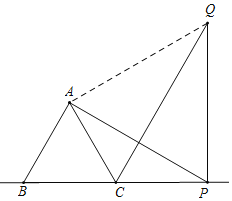
由旋转可得，AP＝QP，∠APQ＝∠ABC＝60°，

∴△APQ是等边三角形，

∴AQ＝PQ，∠APQ＝60°＝∠AQP，

又∵∠APB＝30°，∠ACB＝60°，

∴∠CAP＝30°，∠CPQ＝90°，

∴∠CAP＝∠APA，

∴AC＝PC，

∴△ACQ≌△PCQ，

∴∠AQC＝∠PQC＝∠AQP＝30°，

∴Rt△PCQ中，CQ＝2CP＝8．

综上所述，线段CQ的长为2或8．