题目内容
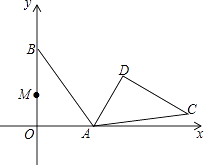
【题目】如图，AB是⊙O的直径，BC是弦，过点O作OE⊥BC于H交⊙O于E，在OE的延长线上取一点D，使∠ODB=∠AEC，AE与BC交于F．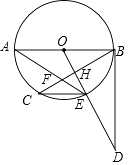 
（1）判断直线BD与⊙O的位置关系，并给出证明；
（2）当⊙O的半径是5，BF=2 
，EF= 
时，求CE及BH的长．
【答案】
（1）解：BD是⊙O的切线；理由如下：
∵∠AEC与∠ABC都对 
，
∴∠AEC=∠ABC，
∵∠ODB=∠AEC，
∴∠ABC=∠ODB，
在Rt△BDF中，∠ODB+∠DBF=90°，
∴∠ABC+∠DBF=90°，即∠OBD=90°，
∴BD⊥OB，
∴BD是⊙O的切线
（2）解：∵∠A=∠C，∠ABF=∠CEF，
∴△CEF∽△ABF，
∴ 
= 
，即 
，
解得：CE= 
；
连接BE，如图所示：
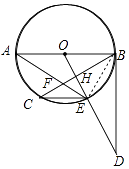
∵AB是⊙O的直径，
∴∠AEB=90°，
∴BE= 
= ，
∴AE= 
= 
，
∴AF=AE﹣EF= ﹣ 
= 
，
∴ 
= 
，
解得：CF= 
，
∴BC=BF+CF= 
，
∵OE⊥BC，
∴BH=CH= 
BC= 
．
【解析】（1）由同弧所对的圆周角相等得到∠AEC=∠ABC，再由已知∠ODB=∠AEC，等量代换得到∠ABC=∠ODB，在直角三角形BDF中，利用直角三角形两锐角互余得到一对角互余，等量代换得到∠OBD为直角，即可得到BD是圆O的切线；（2）证明△CEF∽△ABF，得出对应边成比例求出CE，由勾股定理求出BE和AE，得出AF，求出CF，得出BC的长，由垂径定理得出BH的长．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对垂径定理的理解，了解垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
