题目内容
【题目】如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为 . 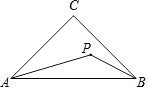
【答案】![]() ﹣1
﹣1
【解析】解:如图所示: 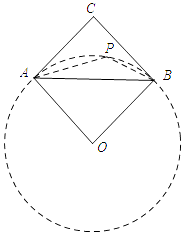
∵在△ABC中,∠C=90°,AC=BC=1,
∴∠CAB=∠CBA=45°.
又∵∠PAB=∠PBC,
∴∠PAB+∠PBA=45°.
∴∠APB=135°.
∴点P在以AB为弦的⊙O上.
∵∠APB=135°,
∴∠AOB=90°.
∴∠OAB=∠OBA=45°.
∴∠CAO=90°.
∴四边形ACBO为矩形.
∵OA=OB,
∴四边形AOBC为正方形.
∴OA=OB=1.
∴OP=1,OC= ![]() .
.
当点O、P、C在一条直线上时,PC有最小值,
∴PC的最小值=OC﹣OP= ![]() ﹣1.
﹣1.
所以答案是: ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目