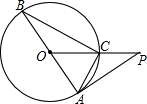
题目内容
如图,⊙O的直径AB=10,C、D是圆上的两点,且 .设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.
.设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.

(1)求证:DF⊥AF.
(2)求OG的长.
 .设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.
.设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.
(1)求证:DF⊥AF.
(2)求OG的长.
(1)证明见解析
(2)OG= 。
。
(2)OG=
 。
。试题分析:(1)连接BD,根据
 ,可得∠CAD=∠DAB=30°,∠ABD=60°,从而可得∠AFD=90°。
,可得∠CAD=∠DAB=30°,∠ABD=60°,从而可得∠AFD=90°。(2)根据垂径定理可得OG垂直平分AD,继而可判断OG是△ABD的中位线,在Rt△ABD中求出BD,即可得出OG。
解:(1)证明:连接BD,

∵AB是⊙O的直径,
 ,
,∴∠CAD=∠DAB=30°,∠ABD=60°。
∵ED是⊙O的切线,∴∠ADF=∠ABD=60°。
∴∠CAD+∠ADF=90°。∴∠AFD=90°。
∴DF⊥AF。
(2)在Rt△ABD中,∠BAD=30°,AB=10,∴BD=5。
∵
 ,∴OG垂直平分AD。
,∴OG垂直平分AD。∴OG是△ABD的中位线,∴OG=
 BD=
BD= 。
。
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
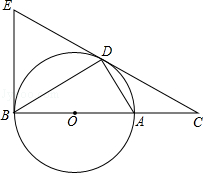
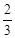 ,求BE的长.
,求BE的长.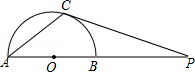





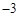
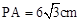 ,求AC的长。
,求AC的长。