题目内容
如图,抛物线经过了边长为1的正方形ABOC的三个顶点A,B,C,则抛物线的解析式为______.
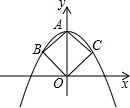

连接BC,交OA于D,则BC⊥OA
在等腰Rt△OAB中,AB=1,∠BAO=∠AOB=45°
∴OA=
,OD=BD=CD=
∴A、B、C三点的坐标分别是(0,
)、(-
,
)、(
,
)
设过A、B、C三点的函数解析式y=ax2+bx+c,可得
,解得
所以抛物线的解析式为:y=-
x2+
.
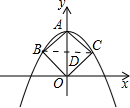
在等腰Rt△OAB中,AB=1,∠BAO=∠AOB=45°
∴OA=
| 2 |
| ||
| 2 |
∴A、B、C三点的坐标分别是(0,
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
设过A、B、C三点的函数解析式y=ax2+bx+c,可得
|
|
所以抛物线的解析式为:y=-
| 2 |
| 2 |


练习册系列答案
相关题目


 份x(月)满足的函数关系如图所示.
份x(月)满足的函数关系如图所示.
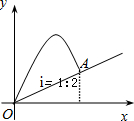

 且与OE平行,现正方形以每秒
且与OE平行,现正方形以每秒