Question

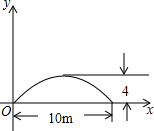
如图，两条钢缆具有相同的抛物线形状．按照图中的直角坐标系，左面的一条抛物线可以用y=0.0225x²+0.9x+10表示，而且左右两条抛物线关于y轴对称．
（1）钢缆的最低点到桥面的距离是______m；
（2）两条钢缆最低点之间的距离是______m；
（3）右边的抛物线解析式是______．

Answer 1

（1）抛物线的顶点坐标为（-

b

2a

，

4ac-b2

4a

），
∴-

b

2a

=-

0.9

2×0.0225

=-20，

4ac-b2

4a

=

4×0.0225×10-0．92

4×0.0225

=1，
故可得左面的一条抛物线的顶点坐标是：（-20，1）．
由顶点的纵坐标为1，可得钢缆的最低点到桥面的距离是1米．
故答案为：1；

（2）由两条抛物线的顶点的横坐标为-20、20，
可得两条钢缆最低点之间的距离是：40米．
故答案为：40；

（3）把y=0.0225x²+0.9x+10中的一次项系数0.9变成相反数，得到：
y=0.0225x²-0.9x+10．
故答案为：y=0.0225x²-0.9x+10．