��Ŀ����
ijˮ��Ʒ��ֳ��ҵΪָ������ҵij��ˮ��Ʒ����ֳ�����ۣ��������г������ˮ��Ʒ��ֳ��������˵��飮���鷢������ˮ��Ʒ��ÿǧ���ۼ�y1��Ԫ���������·�x���£������ϵʽy=-
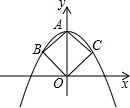
x+36������ÿǧ�˳ɱ�y2��Ԫ���������� ��x���£�����ĺ�����ϵ��ͼ��ʾ��
��x���£�����ĺ�����ϵ��ͼ��ʾ��
��1����ȷ��b��c��ֵ��
��2���������ˮ��Ʒÿǧ�˵�����y��Ԫ���������·�x���£�֮��ĺ�����ϵʽ��
��3������•һ��֮ǰ�����·ݳ�������ˮ��Ʒÿǧ�˵����������������Ƕ��٣�
| 3 |
| 8 |
 ��x���£�����ĺ�����ϵ��ͼ��ʾ��
��x���£�����ĺ�����ϵ��ͼ��ʾ����1����ȷ��b��c��ֵ��
��2���������ˮ��Ʒÿǧ�˵�����y��Ԫ���������·�x���£�֮��ĺ�����ϵʽ��
��3������•һ��֮ǰ�����·ݳ�������ˮ��Ʒÿǧ�˵����������������Ƕ��٣�
��1�������⣺
��ã�
��
��2��y=y1-y2
=-
x+36-��
x2-
x+
��
=-
x2+
x+6
��
��3��y=-
x2+
x+6
=-
(x2-12x+36)+4
+6
=-
��x-6��2+11
��a=-
��0��
�������߿������£�
�ɺ���ͼ��֪���ڶԳ���x=6���y��x�����������
��������x��5��
����4�·ݳ�������ˮ��Ʒÿǧ�˵��������
�������=-
��4-6��2+11=10
��Ԫ����
|
��ã�
|
��2��y=y1-y2
=-
| 3 |
| 8 |
| 1 |
| 8 |
| 15 |
| 8 |
| 59 |
| 2 |
=-
| 1 |
| 8 |
| 3 |
| 2 |
| 1 |
| 2 |
��3��y=-
| 1 |
| 8 |
| 3 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 8 |
��a=-
| 1 |
| 8 |
�������߿������£�
�ɺ���ͼ��֪���ڶԳ���x=6���y��x�����������
��������x��5��
����4�·ݳ�������ˮ��Ʒÿǧ�˵��������
�������=-
| 1 |
| 8 |
| 1 |
| 2 |

��ϰ��ϵ�д�
 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ

 ����A������Ϊ��-4��4����ƽ����x���ֱ��l����0��-1���㣮
����A������Ϊ��-4��4����ƽ����x���ֱ��l����0��-1���㣮