题目内容
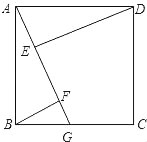
【题目】如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
【答案】详见解析.
【解析】试题分析:由四边形ABCD为正方形,可得出∠BAD为90°,AB=AD,进而得到∠BAG与∠EAD互余,又DE垂直于AG,得到∠EAD与∠ADE互余,根据同角的余角相等可得出∠ADE=∠BAF,利用AAS可得出△ABF≌△DAE;利用全等三角的对应边相等可得出BF=AE,由AF-AE=EF,等量代换可得证.
试题解析:∵ABCD是正方形,
∴AD=AB,∠BAD=90°
∵DE⊥AG,
∴∠DEG=∠AED=90°
∴∠ADE+∠DAE=90°
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠ADE=∠BAF.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在△ABF与△DAE中,
 ,
,
∴△ABF≌△DAE(AAS).
∴BF=AE.
∵AF=AE+EF,
∴AF=BF+EF.

练习册系列答案
相关题目