题目内容
【题目】如图,已知四边形ABCD为矩形,AD=20cm、AB=10cm.M点从D到A,P点从B到C,两点的速度都为2cm/s;N点从A到B,Q点从C到D,两点的速度都为1cm/s.若四个点同时出发.
(1)判断四边形MNPQ的形状.
(2)四边形MNPQ能为菱形吗?若能,请求出此时运动的时间;若不能,说明理由.

【答案】(1)四边形MNPQ是平行四边形, 理由见解析;(2)四边形MNPQ能为菱形时,运动时间是5 s.
【解析】
(1)利用矩形的性质和勾股定理判定四边形MNPQ的两组对边相等,则该四边形为平行四边形;
(2)利用菱形是邻边相等的平行四边形来求运动时间.
(1)解:四边形MNPQ是平行四边形. 理由如下:
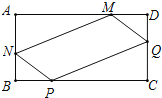
在矩形ABCD中,AD=BC=20cm,AB=CD=10cm,且∠A=∠B=∠C=∠D=90°.
设运动时间为t秒,则AN=CQ=t cm,BP=DM=2t cm.
∴BN=DQ=(10-t)cm,CP=AM=(20-2t)cm.
由勾股定理可得,NP=![]() ,MQ=
,MQ=![]() ,
,
∴NP=MQ.
同理,可得MN=PQ.
∴四边形MNPQ是平行四边形.
(2)能.理由如下:
∵当四边形MNPQ能为菱形时,NP=QP,
∴![]() =
=![]() ,
,
∴![]() ,
,
解得 t=5.
即四边形MNPQ能为菱形时,运动时间是5 s.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目