题目内容
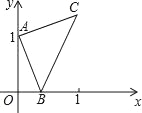
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. 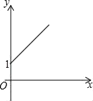 B.
B. 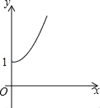 C.
C. 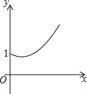 D.
D. 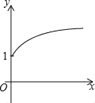
【答案】A
【解析】试题分析:根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.作AD∥x轴,作CD⊥AD于点D,若右图所示,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y, ∵AD∥x轴,
∴∠DAO+∠AOD=180°, ∴∠DAO=90°, ∴∠OAB+∠BAD=∠BAD+∠DAC=90°, ∴∠OAB=∠DAC,
在△OAB和△DAC中,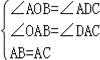 , ∴△OAB≌△DAC(AAS), ∴OB=CD, ∴CD=x,
, ∴△OAB≌△DAC(AAS), ∴OB=CD, ∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1, ∴y=x+1(x>0).

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表如下:

零花钱数额(元) | 5 | 10 | 15 | 20 |
学生个数(个) | a | 15 | 20 | 5 |
请根据表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的众数、中位数和平均数.


