��Ŀ����
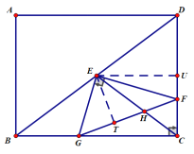
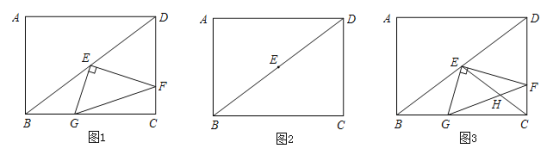
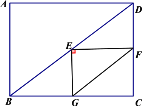
����Ŀ����ͼ1���ھ���ABCD�У�AB=6��BC=8����E�ǶԽ���BD���е㣬ֱ�ǡ�GEF����ֱ�DZ�EF��EG�ֱ�CD��BC�ڵ�F��G��
��1������F�DZ�CD���е㣬��EG�ij���
��2����ֱ�ǡ�GEF��ֱ�Ƕ���E��ת����ת���������CD��BC���ڵ�F��G����EFG�Ĵ�С�Ƿ����仯������仯����˵�����ɣ�������䣬�����tan��EFG��ֵ��
��3����ֱ�ǡ�GEF�ƶ���E��ת����ת���������CD��BC���ڵ�ֱ�߽��ڵ�F��G����ͼ2�л���ͼ�Σ����жϡ�EFG�Ĵ�С�Ƿ����仯������仯����˵�����ɣ�������䣬��ֱ��д��tan��EFG��ֵ��
��4����ͼ3������CE��FG�ڵ�H����![]() �������CF�ij���
�������CF�ij���
���𰸡���1��EG=3����2�����䣬 tan��EFG=![]() ����3�����仯��tan��EFG=
����3�����仯��tan��EFG=![]() ����4��
����4��![]() ��
��
��������
(1)���ݵ�E�ǶԽ��ߵ��е㣬��F��CD���е㣬��֤EF��BC���ٸ�����GEF=90������C=90���ɵ��ı���EGCFΪ���Σ����G��BC���е㣬��ɽ��EG�ij���
��2����EM��CD��M��EN��BC��N���þ���ENCM����֤����GEN�ס�FEM������
![]() ������tan��EFG=
������tan��EFG=![]() ������EFG���仯��
������EFG���仯��
(3)����ͼ�Σ����գ�2���з������̣����ɵó���EFG���仯����tan��EFG=![]() ��
��
(4) ��E�ֱ���ET��GF��T��EU��CD��U����tan��EFG=![]() ����EG=3a��EF=4a��
����EG=3a��EF=4a��
��GF=5a��ET=![]() ��GT=
��GT=![]() ����
����![]() �����FH=
�����FH=![]() ��GH=
��GH=![]() �������ֱ����EH��CH�ij�����֤��FHC�צ�EHG����
�������ֱ����EH��CH�ij�����֤��FHC�צ�EHG����![]() ���ɴ����aֵ�������ֱ�EF��UF�ij����������CF�ij�.
���ɴ����aֵ�������ֱ�EF��UF�ij����������CF�ij�.
��1����E��FΪBD��CD���е�
��EF��BCD�����
��EF=![]() BC=4�� EF��BC
BC=4�� EF��BC
������ABCD����C=90��
���EFC=90��
�ߡ�GEF=90��
���ı���EGCFΪ����
��EG=FC=![]() =3��
=3��
��2�����仯��
��ͼ����EM��CD��M��EN��BC��N���þ���ENCM��
���NEM=90��
�ߡ�GEF=90��
���GEN=��FEM
���GEN�ס�FEM
��![]()
�� tan��EFG=![]() ��
��
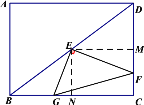
��3����ͼ��ʾ�����仯��tan��EFG=![]() ;
;

���ɣ���EM��CD��M��EN��BC��N���þ���ENCM��
���NEM=90��
�ߡ�GEF=90��
���GEN=��FEM���֡�ENG=��EMF=90��
���GEN�ס�FEM
��![]()
�� tan��EFG=![]() ��
��
(4)��E�ֱ���ET��GF��T��EU��CD��U��
��tan��EFG=![]() ����GEF=90��
����GEF=90��
�ʿ���EG=3a��EF=4a��
��GF=5a��ET=![]() ��GT=
��GT=![]() ��
��
��![]() ��
��
��FH=![]() ��GH=
��GH=![]() ��
��
��HT=GH-GT=![]() -
-![]() =
=![]() ��
��
��EH=![]() =
=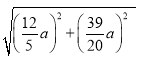 =
=![]() ��
��
�ߡ�BCD=90��BC=8��AB=CD=6��
��BD=10����E��BD���е㣬
��CE=![]() BD=5��
BD=5��
��CH=CE-EH=5-![]() ��
��
��tan��CE=![]() ��tan��EGF=
��tan��EGF=![]() ��
��
���UCE=��EGF������CHF=��EHG��
�তFHC�צ�EHG��
��![]() ����
����![]() ��
��
��![]() ��(5-
��(5-![]() )=
)=![]() ��
��![]() ��
��
��![]() ��
��
��EF=![]() ��
��
��UF=![]() =
=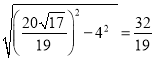 ��
��
��CF=CU-UF=3-![]() =
=![]() .
.