题目内容
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大请将他们的探究过程补充完整。
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=_________。
(2)上述函数表达式中,自变量x的取值范围是____________;
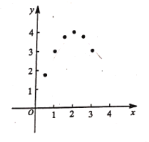
(3)列表:
x | ... | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | ... |
y | ... | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | ... |
写出m=__________;
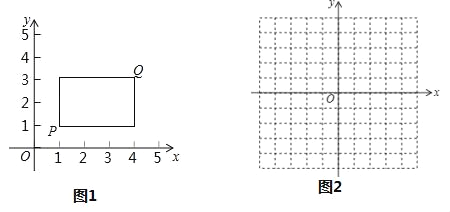
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得:x=_______时,矩形的面积最大: 写出该函数的其它性质(一条即可):_______________________________________.
【答案】(1)-x2+4x;(2)0<x<4;(3)1.75;(4)见解析;(5)2,当0<x<2时,y随x增大而增大.
【解析】
(1)根据矩形的周长=2(长+宽),矩形的面积=长×宽,即可列出函数表达式;
(2)根据y=-x2+4x,-x2+4x>0即可得出答案;
(3)把x=3.5代入解析式计算即可得;
(4)根据表格中的坐标描点画图即可;
(5)结合图象可得x=2时,y有最大值,再根据函数的解析式及图象写出一条性质即可.
(1)∵矩形的周长=2(长+宽),矩形的面积=长×宽,
又∵矩形的周长为8,面积为y,矩形的一边长为x,
∴由题意:y=x(4-x)=-x2+4x;
(2)∵y=-x2+4x,
∴x>0,且-x2+4x>0,
又∵-x2+4x>0解得x>0,x<4,
则自变量x的取值范围是0<x<4;
(3)x=3.5时,y=1.75,
∴m=1.75;
(4)函数图象如图所示:
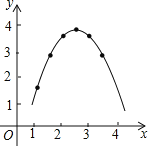
(5)∵y=-(x-2)2+4,
∴x=2时,y有最大值,
性质:当0<x<2时,y随x的增大而增大.(答案不唯一).