题目内容
【题目】方程是刻画现实世界的有效模型,表格是建立方程的策略之一.请填写表格数据,并列方程解决问题.轮船和汽车都从甲地开往乙地,海路比公路近40千米,轮船上午7点开出,速度是每小时24千米.汽车上午10点开出,速度为每小时40千米,结果同时到达了乙地.求甲、乙两地的海路和公路长.
速度 | 时间 | 路程 | |
汽车 | 40 |
| x |
轮船 | 24 |
|
|
【答案】![]() ;
;![]() ;x﹣40;方程见解析;海路长240千米,公路长280千米.
;x﹣40;方程见解析;海路长240千米,公路长280千米.
【解析】
设从甲地开往乙地的公路长x千米,则从甲地开往乙地的海路长(x﹣40)千米,乘汽车所需时间为![]() ,乘轮船所需时间为
,乘轮船所需时间为![]() ,根据乘轮船比乘汽车多用3个小时,即可得出关于x的一元一次方程,解之即可得出结论.
,根据乘轮船比乘汽车多用3个小时,即可得出关于x的一元一次方程,解之即可得出结论.
解:设从甲地开往乙地的公路长x千米,则从甲地开往乙地的海路长(x﹣40)千米,乘汽车所需时间为![]() ,乘轮船所需时间为
,乘轮船所需时间为![]() ,
,
依题意,得:![]() +3=
+3=![]() ,
,
解得:x=280,
∴x﹣40=240.
答:海路长240千米,公路长280千米.
故答案为:![]() ;
;![]() ;x﹣40.
;x﹣40.

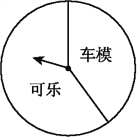
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?