题目内容
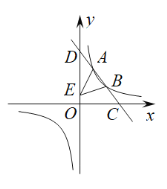
【题目】如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′ 的度数是______________.
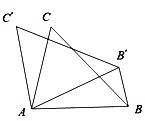
【答案】105°
【解析】
根据旋转的性质得AB′=AB,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AB′B=∠ABB′,然后根据平行线的性质得到∠AB′B=∠C′AB′=75°,于是得到结论.
解:∵△ABC绕点A逆时针旋转到△AB′C′,
∴AB′=AB,∠B′AB=∠C′AC,∠C′AB′=∠CAB=75°,
∴△AB′B是等腰三角形,
∴∠AB′B=∠ABB′
∵BB'∥AC,
∴∠A B′B=∠C′AB′=75°,
∴∠C′AC=∠B′A B =180°-2×75°=30°,
∴∠BAC′=∠C′AC+∠BA C =30°+75°=105°,
故答案为:105°.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目