题目内容
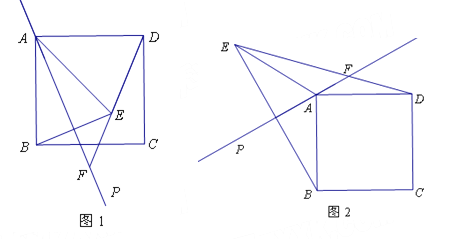
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.

【答案】(1)证明见解析;(2)S△ABC=![]() 或
或![]() ;(3)b2=ac.
;(3)b2=ac.
【解析】试题分析:(1)欲证明PA是切线,只要证明PA⊥OA即可;
(2)分两种情形分别求解即可;
(3)只要证明AD∥OB,可得△AED∽△OEB,推出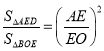 ,再推出
,再推出![]() 可得
可得![]() =(
=(![]() )2,b2=ac.
)2,b2=ac.
试题解析:
(1)证明:∵BD=BC,
∴∠BDC=∠BCD,
∵∠P=∠BCD,∠BAC=∠BDC,
∴∠P=∠BAC,
∵AC是直径,
∴∠ABC=∠ABP=90°,
∴∠P+∠BAP=90°,
∴∠BAP+∠BAC=90°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)解:①当∠OED=90°时,CB=CD=BD,△ABC是等边三角形,可得∠ACB=30°,
∵AC=2,
∴AB=1,BC=![]() ,
,
∴S△ABC=![]() .
.
②当∠DOE=90°时,易知∠AOB=45°,△ABC的AC边上的高=![]() ,
,
∴S△ABC=![]() .
.
(3)∵BD=BC,OD=OC,BO=BO,
∴△BOD≌△BOC,
∴∠OBD=∠OBC,
∵OB=OD=CO,
∴∠OBD=∠OBC=∠ODB=∠OCB,
∵∠ADB=∠OCB,
∴∠ADB=∠OBD,
∴AD∥OB,
∴△AED∽△OEB,
∴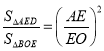 ,
,
∵![]() ,
,
∴![]() =(
=(![]() )2,
)2,
∴b2=ac.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目