题目内容
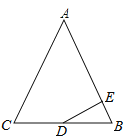
【题目】已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
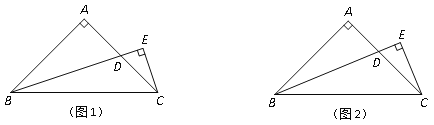
(1)若BD是AC边上的中线,如图1,求![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求![]() 的值.
的值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】
设AB=AC=1,CD=x,应用勾股定理和相似三角形的判定和性质,把![]() 用x来表示,
用x来表示,
(1)若BD是AC的中线,则CD=AD,据此求出![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,则由Rt△ABD∽Rt△EBC得![]() ,据此求出
,据此求出![]() 的值.
的值.
设AB=AC=1,CD=x,则0<x≤1,BC=![]() ,AD=1-x.
,AD=1-x.
在Rt△ABD中,BD2=AB2+AD2=1+(1-x)2=x2-2x+2.
由已知可得Rt△ABD∽Rt△ECD,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
∴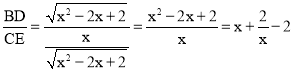 ,0<x≤1.
,0<x≤1.
(1)若BD是AC的中线,则CD=AD=x=![]() ,得
,得![]() .
.
(2)若BD是∠ABC的角平分线,则Rt△ABD∽Rt△EBC,
∴![]() ,得
,得![]() ,即
,即![]() ,解得,
,解得,![]() .
.
∴![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】赣县田村素称“灯彩之乡”,田村花灯源于唐代,盛于宋朝,迄今已有1300多年历史了,某公司生产了一种田村花灯,每件田村花灯制造成本为20元.设销售单价x(元),每日销售量y(件)、每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
销售单价x(元) | 30 | 31 | 32 | 40 |
销售量y(件) | 40 | 38 | 36 | 20 |
(1)根据表中数据的规律、分別写出每日销售量y(件)、每日利润w(元)关于销售单价x(元)之间的函数表达式(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?