题目内容
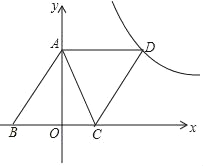
【题目】如图,直线y=﹣2x+4与x轴,y轴分别交于点C,A,点D为点B(﹣3,0)关于AC的对称点,反比例函数y=![]() 的图象经过点D.
的图象经过点D.
(1)求证:四边形ABCD为菱形;
(2)求反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
【答案】(1)证明见解析;(2)反比例函数解析式为y=![]() ;(3)点M的坐标为(0,
;(3)点M的坐标为(0,![]() ).
).
【解析】
(1)由直线解析式可得A(0,4),C(2,0),利用勾股定理求得AB=5=BC,又由D为B点关于AC的对称点,可得AD=AB=5,CD=CB=5,即可证得AB=BC=CD=DA,得证四边形ABCD为菱形.
(2)由四边形ABCD为菱形.可求得点D的坐标,然后利用待定系数法即可求得此反比例函数的解析式.
(3)由四边形ABMN是平行四边形,根据平移的性质可得到N的横坐标,代入反比例函数解析式求出N纵坐标,从而求得M的坐标.
解:(1)∵直线y=﹣2x+4与x轴,y轴分别交于点C,A,
∴A(0,4),C(2,0),
∴AB=![]() =5,BC=5,
=5,BC=5,
∵D为B点关于AC的对称点,
∴AD=AB=5,CD=CB=5,
∴AB=BC=CD=DA,
∴四边形ABCD为菱形.
(2)∵四边形ABCD为菱形,
∴AD∥BC,
而AD=5,A(0,4),
∴D(5,4),
把D(5,4)代入y=![]() 得k=5×4=20,
得k=5×4=20,
∴反比例函数解析式为y=![]() .
.
(3)∵四边形ABMN是平行四边形,
∴AB∥NM,AB=NM,
∴MN是AB经过平移得到的,
∵点M是点B在水平方向向右平移3个单位长度,
∴点N的横坐标为3,代入y=![]() 中,得:y=
中,得:y=![]() ,
,
∴点M的纵坐标为![]() ﹣4=
﹣4=![]() ,
,
∴点M的坐标为(0,![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
【题目】某产品每件成本10元,试销阶段每件产品的销售价![]() (元)与产品日销售量
(元)与产品日销售量![]() (元)间的关系如下:
(元)间的关系如下:
| … | 12 | 15 | 18 | 21 | 24 | … |
| … | 28 | 25 | 22 | 19 | 16 | … |
日销售量![]() 是销售价
是销售价![]() 的一次函数.
的一次函数.
(1)求出日销售量![]() (件)与销售量
(件)与销售量![]() (元)的函数关系式.
(元)的函数关系式.
(2)要使每日的销售利润200元,每件产品的销售应定为多少元?进货成本多少元?
(3)选作:要使每日的销售的利润最大,每件产品的销售价应定为多少元?
【题目】某学校为了了解在校初中生阅读数学文化史类书籍的现状,随机抽取了初中部部分学生进行研究调查,依据相关数据绘制成以下不完整的的统计图表,请你根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | C |
说不清楚 | 9 | 0.06 |
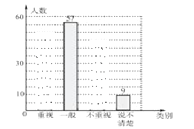
(1)求表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2400名,请估计该校“不重视”阅读数学文化史书籍的初中生人数;
(3)若小明和小华去书店,打算从A,B,C,D四本数学文化史类书籍中随机选取一本,请用画树状图或列表格的方法,求两人恰好选中同一本书籍的概率。